Array Geometries and the Analyzable Quantities

What Array Geometries Is BIDO Good for?

BIDO's array analysis theory is based on the assumption of a circular array installed on the ground surface (with sensors at all locations around a circle). In practice, however, problems arise as to how many sensors should be installed around the circle and whether or not a sensor should be installed at the center. To make a shortcut to the conclusion, BIDO can be applied to arrays of 0, 1, 2, 3 or 5 (or odd numbers of) sensors around a circle. An array can consist of a maximum number of 6 sensors if one of them is installed at the center. The range of analyzable quantities differ for different array geometries and record components.

The following describes the correspondence relations between the array geometries, record components and the analyzable quantities. The table lists the names of the quantities that can be analyzed and of the analysis methods that can be implemented.

Array geometry (Black circles: sensors)
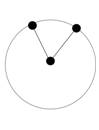
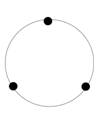
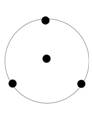
Total number of sensors		1	2	3	3	4	5	6
At the center		1	1	1	0	1	0	1
Around the circle		0	1	2	3	3	5	5
Vertical motion alone	Phase velocities of Rayleigh waves	None	SPAC	SPAC H0	CCA	SPAC CCA nc-CCA H0, H1, V	CCA	SPAC CCA nc-CCA H0, H1, V
	Phase velocities of Love waves	None	None	None	None	None	None	None
	Other quantities	PSD	PSD	PSD	PSD	PSD NSR(V)	PSD	PSD NSR(V)
Horizontal motion alone	Phase velocities of Rayleigh waves	None	None	None	CCA-R	CCA-R SPAC-R SPAC+R	CCA-R	CCA-R SPAC-R SPAC+R
	Phase velocities of Love waves	None	None	None	CCA-L	CCA-L SPAC-L SPAC+L	CCA-L	CCA-L SPAC-L SPAC+L
	Other quantities	PSD	PSD	PSD	PSD	PSD NSR(H)	PSD	PSD NSR(H)
Three-component	Phase velocities of Rayleigh waves	None	SPAC	SPAC H0	CCA CCA-R	SPAC CCA nc-CCA H0, H1, V CCA-R SPAC-R SPAC+R	CCA CCA-R	SPAC CCA nc-CCA H0, H1, V CCA-R SPAC-R SPAC+R
	Phase velocities of Love waves	None	None	None	CCA-L	CCA-L SPAC-L SPAC+L	CCA-L	CCA-L SPAC-L SPAC+L
	Other quantities	PSD H/V	PSD H/V	PSD H/V	PSD H/V	PSD H/V R/V, R/L NSR(V) NSR(H)	PSD H/V	PSD H/V R/V, R/L NSR(V) NSR(H)

(Notes)

- SPAC: Spatial Autocorrelation method・(its more generalized variant is applicable to horizontal motion, but here, the term is used to denote "the method to analyze phase velocities of Rayleigh waves using vertical motion)

- CCA: A method to analyze phase velocities of Rayleigh waves using vertical motion (reference [1, 3])

- nc-CCA, H0, H1, V: Methods to analyze phase velocities of Rayleigh waves using vertical motion (reference [4])

- CCA-R, SPAC-R, SPAC+R: Methods to analyze phase velocities of Rayleigh waves using horizontal motion (reference [5])

- CCA-L, SPAC-L, SPAC+L: Methods to analyze phase velocities of Love waves using horizontal motion (reference [5])

- PSD: Power-spectral densities

- H/V: H/V spectra (Power ratios of horizontal motion to vertical motion)

- NSR(V): Noise-to-signal ratios of the vertical component (reference [3])

- NSR(H): Noise-to-signal ratios of the horizontal components (reference [8])

- R/V: Horizontal-to-vertical amplitude ratios (NOT power ratios) of the Rayleigh waves (reference [2])

- R/L: Rayleigh-to-Love power ratios (reference [5, 7])

As shown in the above table, BIDO allows one not only to analyze array data but also data from single-station measurements, linear arrays of two stations and L-shaped arrays of three stations. (It can also cope with huddle tests where more than one seismic sensors are assigned to a single location). What we had in mind during the early phase of development was the analysis of circular-array data, but we later came to realize that, at real measurement sites (especially in urban areas), simpler array geometries are preferred because of their ease of installation. It is coming to be known that linear arrays and L-shaped arrays can be applied to the analysis of vertical motion in a number of cases, and so we decided to incorporate these into BIDO. The third and fourth columns on the left-hand side of the table both refer to arrays of three seismic sensors, but the range of applicable methods differ according to whether one of the sensors is regarded as assigned to the center of the circular array or whether all of them are regarded as lying around the periphery of the circle.

It goes without saying, though, that larger numbers of sensors around the circle produce higher precision and more stable analysis results. We recommend the installation of six-sensor arrays, as shown in the right-hand column of the table, when small arrays (10 m or less in radius) are to be used. Particularly, when using miniature arrays of around 1 m in radius (see photos in the top page), six-station arrays are expected to an effective design not only in terms of high precision but also in terms of efficiency (see One Approach to Make the Most of the Method's Potential).

Notes on the Array Analysis of Horizontal Motion

Array analysis of horizontal motion is currently still on the level of basic research. It has been shown that Love wave velocities and other properties can be analyzed using an array of five sensors around a circle and another at its center (references [5, 7]), but the extent of reliability of the analysis results from arrays with only three sensors around a circle remains yet to be studied. BIDO is designed in such a way that the analysis of horizontal motion is possible even when the array has only three sensors around the circle, but this feature is intended principally for the developer, and considerable caution is required in interpreting the analysis output. Caution is also necessary when S/N ratios are low (noise is large), because this considerably impairs the reliability of analysis results even when five sensors are installed around the circle. Unfortunately, there is, so far, no established theoretical rationale for assessing the reliability of analysis results for horizontal motion on the basis of S/N ratio estimates.

On Deviations from a "Circular" Array

When using circular arrays with three or more sensors around a circle, the stations do not necessarily have to be installed at equal intervals around the circle (reference [2]), but equidistant arrays are preferred to ensure high precision. There is no theory of correction for stations that do not lie on the circle (location errors in the radial direction), so the program sets a default allowance limit of 5% for such errors (modifiable by program recompilation) and regard the stations as lying on the circle.

[RETURN] [BIDO TOP]