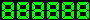Control of Underactuated Manipulators

Introduction

The concept of minimalism, performing a given class of tasks by the simplest devices taking advantage of the task dynamics, is an important issue in robot manipulation. For example, if control of manipulators with more degrees of freedom than the number of actuators is feasible, weight, cost and energy consumption of manipulators can be reduced. It can also be useful in fault tolerance of manipulator control.

Utilizing Dynamic Coupling
We have been investigating control of underactuated manipulators utilizing dynamic coupling. The passive joints were equipped with holding brakes instead of actuators. When the brake is engaged, the active joint can be controlled without affecting the state of the passive joint. When the holding brake is released, the passive joint can rotate freely and is controlled indirectly by using the coupling characteristics of manipulator dynamics. The position of the manipulator is controlled by combining these two control modes.

Point to Point Control
In point to point control, mode switching is performed twice. First, the passive joint is fixed and the active joint is accelerated. Next, the passive joint is released and the passive joint is positioned to the desired angle. Finally, the passive joint is fixed again the active joint is positioned. This method is extended to path tracking control. The manipulator is controlled to follow a geometrically specified path. A "path coordinate system" is defined in operational space. The path coordinates consist of a component parallel to the path and a component normal to the path. The component normal to the desired path is controlled to suppress tracking error. This in turn keeps the manipulator on the desired path.
(video 1).

Nonholonomic Control

The above methods required brakes at the passive joints for positioning. However, the nonholonomic constraints on such manipulators indicate the possibility of the positioning using no brakes. The nonholonomic constraints on underactuated manipulators have different characteristics from those of wheeled vehicles and space robots etc., which have been studied as typical nonholonomic systems. These examples have kinematic constraints, which geometrically limit the direction of mobility, or dynamic constraints caused by conservation of angular momentum. These constraints can be represented as a differential equation including the generalized coordinates and the generalized velocities. On the other hand, the dynamic constraints introduced by passive joints are also functions of the generalized accelerations and are called second-order nonholonomic constraints. These constraints make it difficult to directly apply the mathematical techniques so far developed for first-order nonholonomic systems.

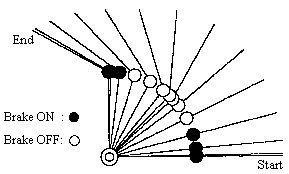
Experimental Setup
We investigated control of a horizontal 3-DOF underactuated manipulator with the third joint being passive. The experimental manipulator has two active joints and one passive joint. The lengths of the links are 0.3m each. The first and the second joints are actuated by 35W and 20W DC servo motors, respectively. The third joint is passive and has neither an actuator nor a brake. The angle of each joint is detected by the use of a rotary encoder. A personal computer (80486CPU, 50MHz) is used as the controller. The objective of the control is to manipulate the position and orientation of the link using the nonholonomic constraint.
It should be noted that the linear approximation of this manipulator is not controllable, while that of an underactuated mechanism in vertical plane, e.g. an inverted pendulum, is controllable due to gravity. This system is equivalent to a planar rigid body sliding on a horizontal frictionless plane, a point of which a force of arbitrary direction and magnitude can be applied. The same dynamics are found in pushing manipulation of a object, a hovercraft, and an omnidirectional tractor connected to a ball-caster trailer.

Trajectory Planning

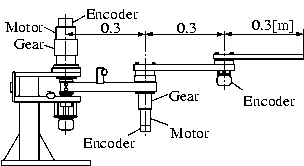
The basic algorithm to plan the trajectory for positioning is as follows. First, simple trajectory segments are built, along which components of the generalized coordinates can be decoupled. Then a trajectory from the initial configuration to the desired configuration is composed of these trajectory segments. Even when the active joints stop and the accelerations become zero, the passive joint generally continues moving due to the inertia. Therefore, the trajectory segments should be special trajectories along which the active and passive joints simultaneously stop.

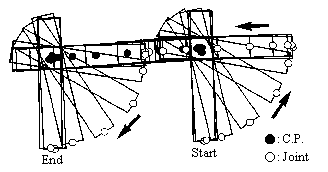
It is obvious that no angular acceleration occurs at the free link when the passive joint is accelerated or decelerated in the direction of the center of gravity of the link. The link can be translated without rotation by this motion. When the joint is rotated around the center of percussion (C.P.) of the link with regard to the joint, the C.P. stays still. The link can then be rotated without translation.

The trajectory from an arbitrary initial configuration to an arbitrary desired configuration can be composed of these trajectory segments. The positioning between the initial configuration and the desired configuration is as follows. First, the joint moves along the rotational trajectory around the C.P. of the link. Then the joint is accelerated towards the center of gravity and the link moves straight along the translational trajectory. Finally, the joint rotates along the rotational trajectory to the desired configuration.
If the initial and the desired orientations of the link are not parallel, the positioning trajectory can be constructed in a different way. First, the link moves along the translational trajectory. Next, the link rotates around the C.P. along the rotational trajectory. Finally, the joint moves along the translational trajectory. Thus, the link can reach the desired configuration from the initial configuration.

Feedback Control

If the position of the passive joint is rigorously controlled according to the desired trajectory, the orientation of the free link also tracks the trajectory and positioning is achieved. However, both types of trajectory segments are unstable and increase the error of the orientation as shown in the video. In addition, the friction of the passive joint, the modeling error of the free link, and the tracking error of the passive joint position may cause the error of the orientation in the real robot. Consequently, feedback control is essential to suppress such errors.

A horizontal underactuated manipulator cannot be asymptotically stabilized to an equilibrium point by any smooth state feedback, based on Brockett's theorem. In other words, no state feedback law can stabilize the position and orientation of free link simultaneously to the desired configuration. Here, the objective of the feedback control is changed to stabilize the free link to the desired trajectory, instead of the desired point.

The nonlinear feedback control we used is based on the following idea. In the case of a translational trajectory, the acceleration of the passive joint in the direction of the desired trajectory gives rise to the inertial force on the free link in the opposite direction. Then the link has the same dynamics as a pendulum or an inverted pendulum in a virtual gravity field. Feedback to stabilize the orientation and position of the link to the desired trajectory can be designed using the acceleration normal to the desired trajectory as the input. Exact linearization of the system and linear state feedback are employed for stabilization. In case of the rotational trajectory, feedback can be constructed by treating the centrifugal force as virtual gravity (video 2) (video 3).

Publications

Research projects
Arai's page