NURBS曲線・曲面NURBSとは曲線・曲面の表現形式の一種で、Bスプライン曲線・曲面やベジエ曲線・曲面を一般化したものです。Wikipediaでの解説(英語)は こちら。 以下の内容は、学生時代(1997年頃)に勉強した内容を研究室のホームページで公開していたものを再編集したものです。 「曲線の性質」ではNURBS曲線の性質を自分が理解するために行ったテスト結果を記しています。 学生時代に参考文献を読んで処理を自分で実装して実験を行った内容です。 この当時は研究室にあったSunのワークステーション上で、C言語でプログラムを書いて、 結果をテキストで出力してそれをgnuplotで表示して確認していました。 「概要」の図は、その後(1998年頃)にSunのワークステーション上でOpenGLで描画するプログラムを書いてから描画した例です。 概要NURBS曲線・曲面はパラメトリック曲線・曲面の一種で、Bスプライン曲線・曲面やベジエ曲線・曲面を一般化したものです。それらと同様に、離散的な制御点の並びによって連続的な曲線・曲面を表現します。Bスプラインからの拡張としては、円弧や球面を表現できる点が挙げられます。 下図はNURBS曲線で円を表現した例です。曲線は始点から終点まで1次元のパラメータ上で定義されますが、 円を表現する場合は始点と終点の制御点を一致させて幾何的に接続しています。 
下図はある平面曲線を平面と直交方向に押し出して作成したNURBS曲面の例を示しています。 曲面は2次元のパラメータ平面上で定義されるので、 通常のNURBS曲面はこのように格子状に配置された制御点で定義されます。 
下図はNURBS曲面でトーラス面を表現した例です。一見わかりにくいと思いますが、 格子状に配置された制御点の向かい合う辺同士を空間上で接続するとこのような面が表現できます。 2つのパラメータ方向の断面がそれぞれ円になるので、これもBスプライン曲面では表現できません。 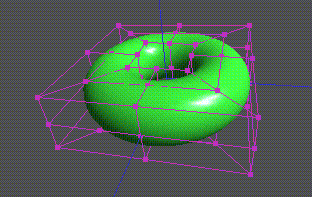
定義ここではNURBS曲線・曲面の定義を示します。 NURBSはNon-Uniform Rational B-Splineの略で、日本語に直すと「非一様有理Bスプライン」となります。
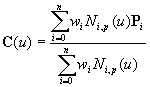

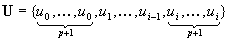
曲線はn+1個の制御点とウェイト、n+p+2個のノットからなるノットベクトルで定義されます。 ただし、pは次数(位数)を示します。ノットベクトルで曲線セグメントの区間幅を変化させられるので、 「非一様」と呼ばれます。また、各制御点の基底関数が基底関数全体の総和で割られているので 「有理」となります。 曲線の式を書き直すと以下のように表せます。 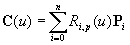
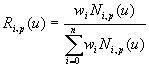
このRを有理基底関数と呼びます。 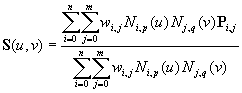
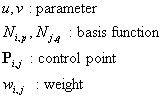
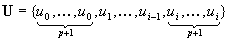
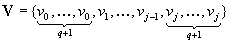
曲面は(n+1)×(m+1)個の制御点とウェイト、n+p+2個とm+q+2個のノットからなる2つのノットベクトルで定義されます。 ただし、pはu方向の次数(位数)を、qはv方向の次数(位数)を示します。 上記で用いられる有理でない基底関数は次式で表されます。 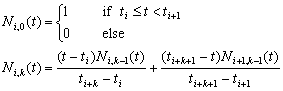
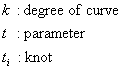
この基底関数はノットの集合であるノットベクトルで定義されます。 ノット値は単調増加な実数列である必要があります。 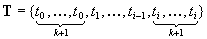
ここに示すように、両端に所定の多重度でノットを指定すると、曲線の両端点や曲面の四隅の点が制御点と一致します。 曲線の性質:次数(位数)ここでは制御点とウェイトが同一で次数(位数)pが異なる曲線を示します。 制御点の配置は下図のように指定します。 
各pに対応する有理基底関数は次のようになります。 まずp=2のときです。 ノットベクトルは {0, 0, 0, 0.2, 0.4, 0.6, 0.8, 1, 1, 1}とします。 これは、パラメータの定義域を0から1として次数に応じて両端を多重化し、 残りのノット値は必要な区間数で定義域を均等に割ることで決定しています。 以降でも同様です。 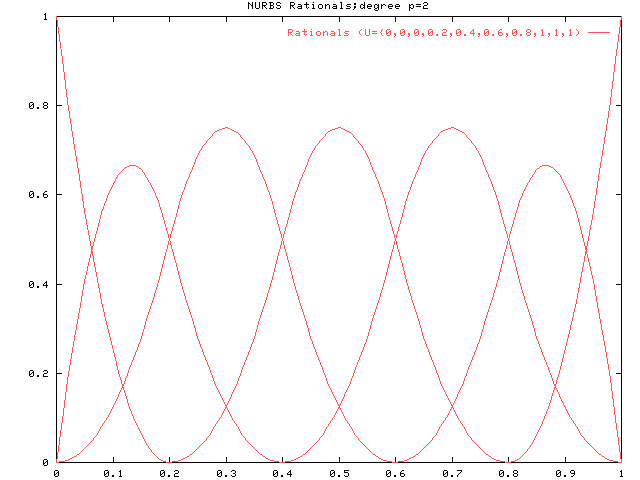
次にp=3のときです。 ノットベクトルは{0, 0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1, 1}です。 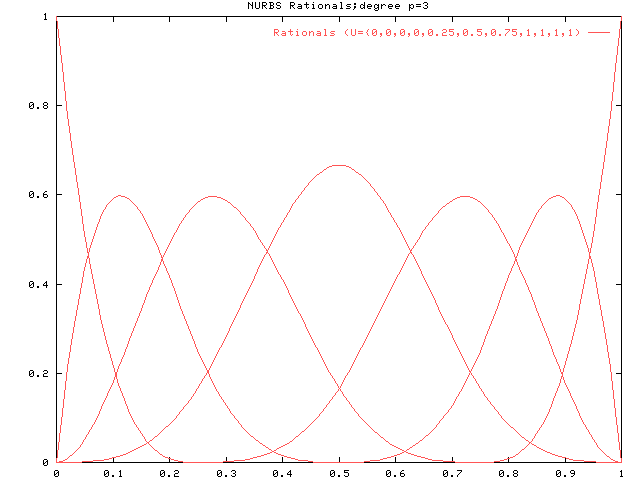
最後にp=4のときです。 ノットベクトルは {0, 0, 0, 0, 0.33, 0.67, 1, 1, 1, 1}です。 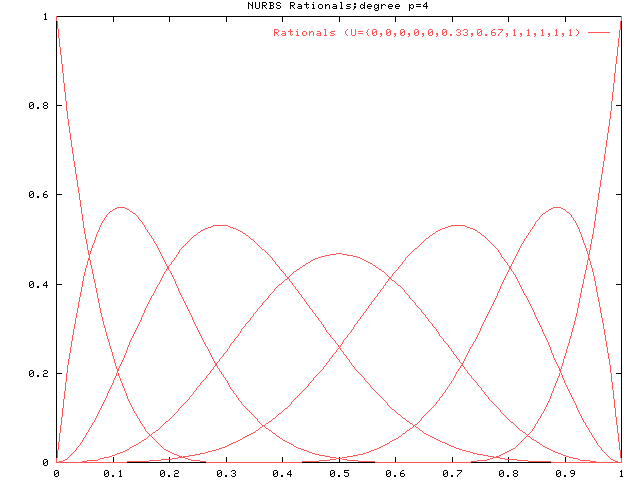
下図は上記すべての有理基底関数を重ねて比較したものです。 ノットの数は異なりますが、有理基底関数の山の数は同じであることがわかります。 基底関数の山は各制御点に対応しているので、このような形になります。 一方、次数が上がると有理基底関数の山のすそが広がっていることがわかります。 ノットの数が少ないと曲線のセグメント数が少なくなって、各基底関数の存在範囲が広がります。 これは次数が上がると、一つの制御点が影響を与える範囲が広くなることを意味します。 見方を変えると、一つのセグメントに影響を与える制御点の数が多くなるとも言えます。 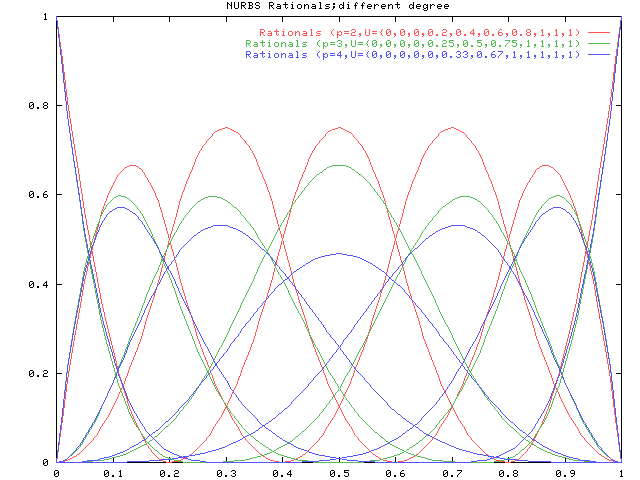
すべての曲線を重ねて表示した図は以下になります。 次数が上がると曲線が制御点の並びから徐々に離れていく様子がわかります。 これは一つのセグメントに影響を与える制御点の数が多くなるからです。 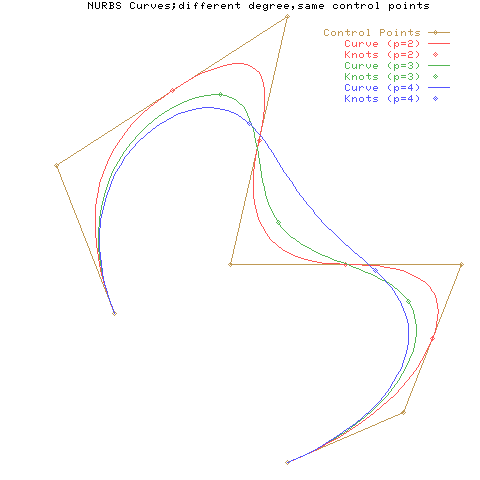
曲線の性質:制御点ここでは制御点が動いたときの曲線の変化について示します。 まずp=2の場合です。 制御点が動いても、有理基底関数は変わりません。 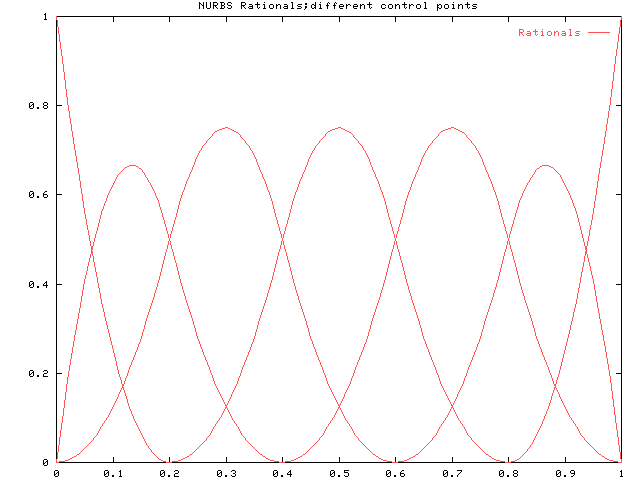
1つの制御点を3パターンで動かしたときの曲線の様子です。 曲線の端点側の2つのセグメントは変化していません。 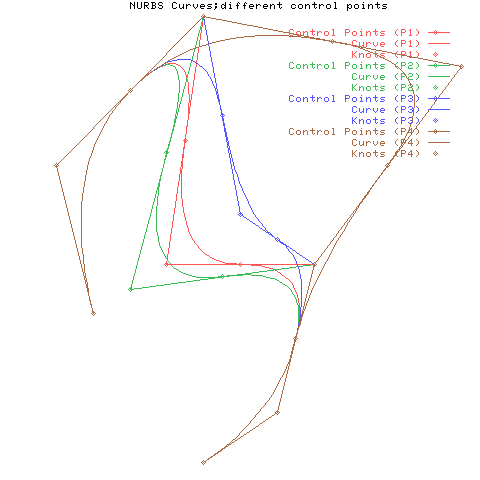
続いてp=3の場合です。 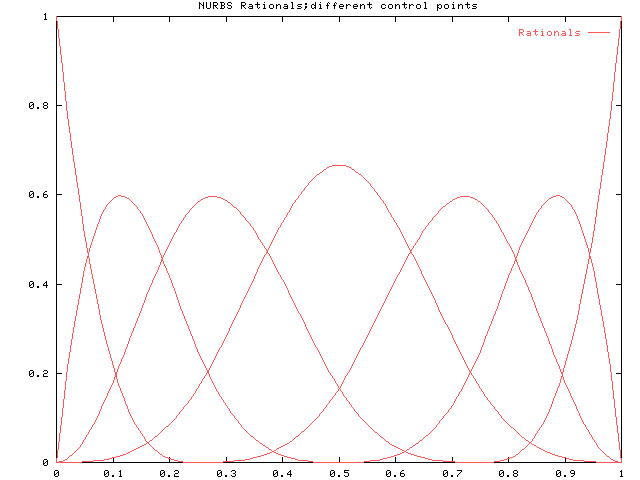
ここでは1つの制御点を2パターンで動かしたときの曲線の様子を示します。 曲線全体が変化していて、次数が上がったため影響範囲が広がったことがわかります。 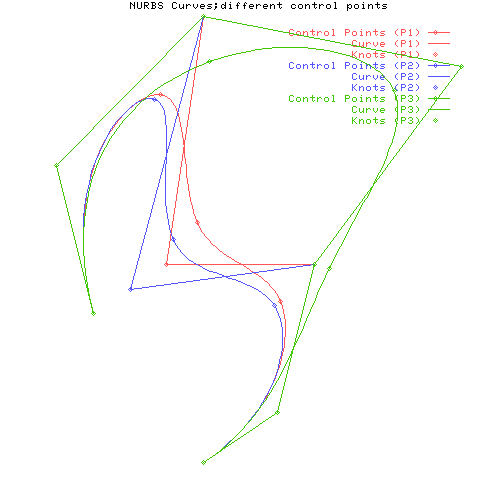
曲線の性質:ウェイトここではウェイトが変化したときの曲線の様子を示します。 p=2の場合です。 下図はすべてのウェイトが1のときの有理基底関数です。 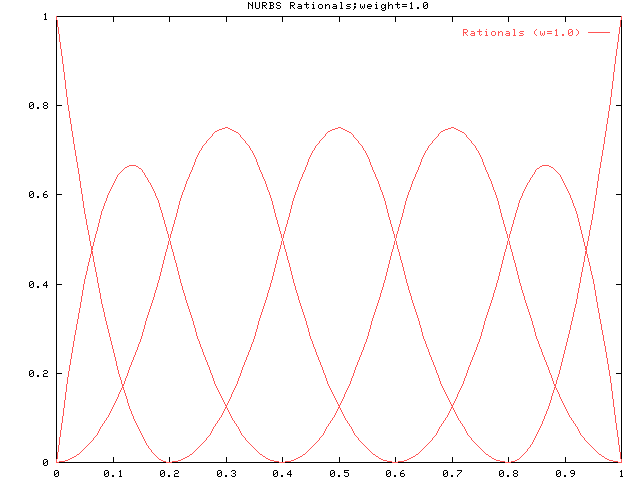
上記について中央の山に対応するウェイトを変化させます。 下図はウェイトを2にした場合です。 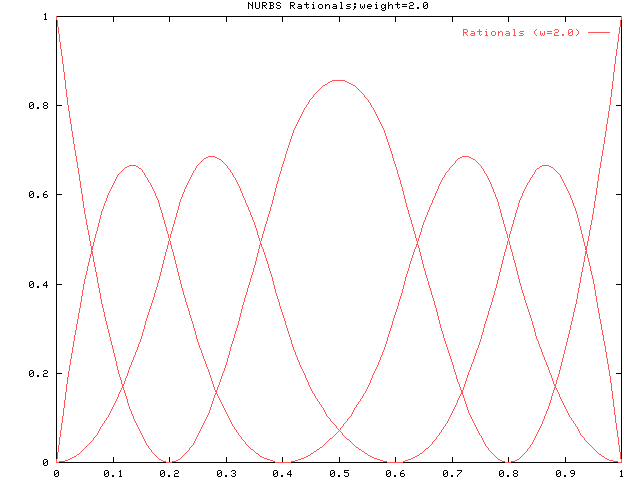
次にウェイトを0.5にした場合です。 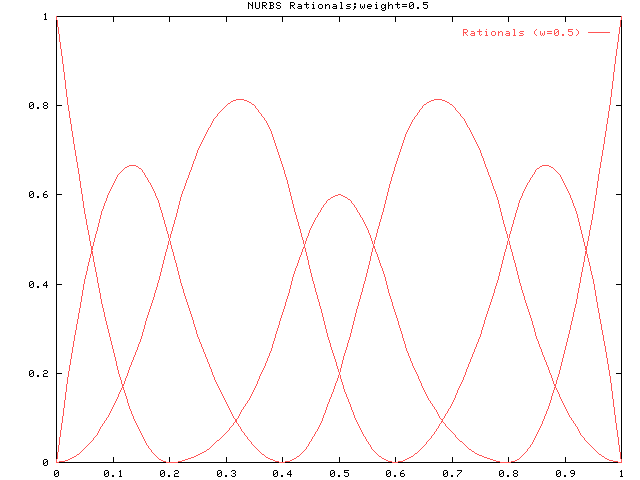
最後にウェイトを0にした場合です。 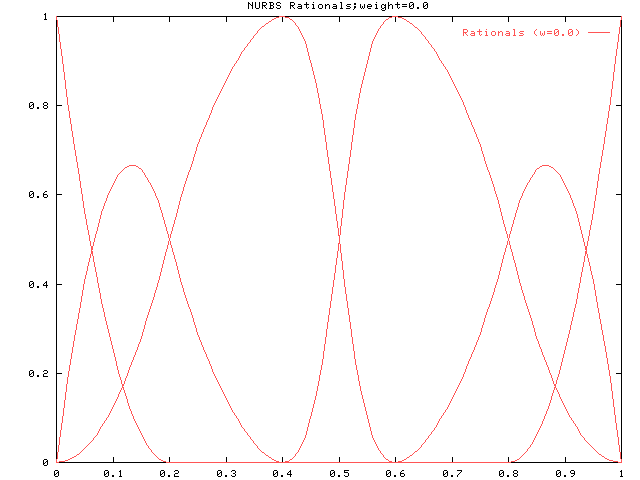
下図は上記の有理基底関数を重ねて比較したものです。 有理基底関数の変化した範囲は0.2から0.8の区間に限定されています。 これは中央の山が存在する範囲に対応します。 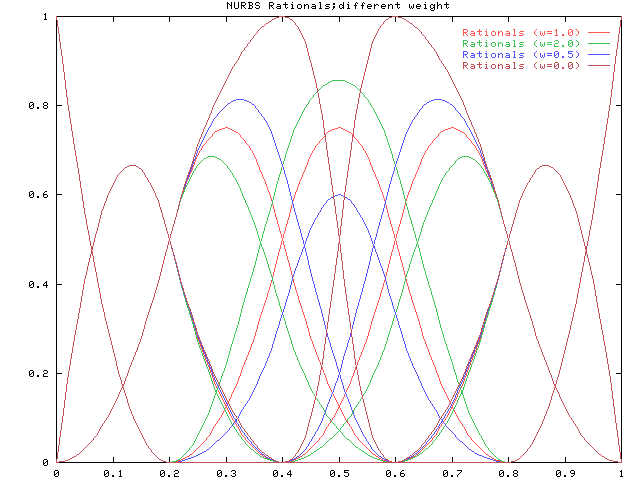
ウェイトを変化させたときの曲線の様子を示します。 ウェイトが大きくなると、曲線は対応する制御点に近くなり、 ウェイトが小さくなると制御点から遠くなる様子がわかります。 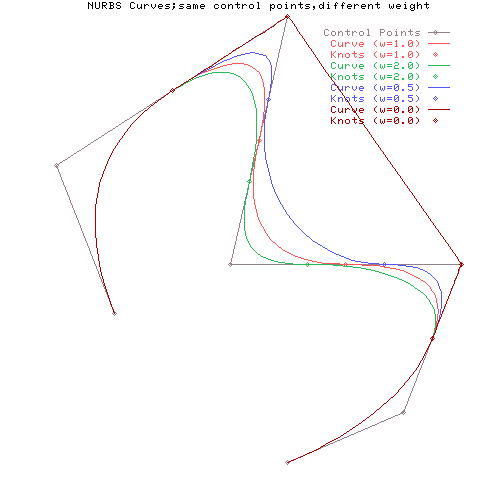
同様にp=3の場合です。 ウェイトがすべて1の有理基底関数です。 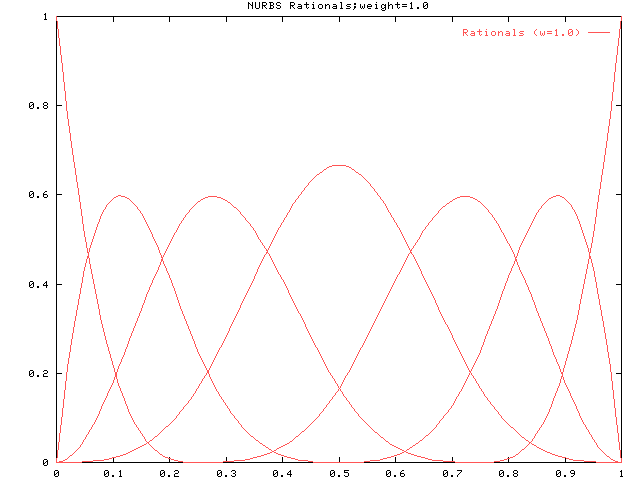
上記に対して中央の山に対応するウェイトを変化させます。 まずはウェイトを2にした場合です。 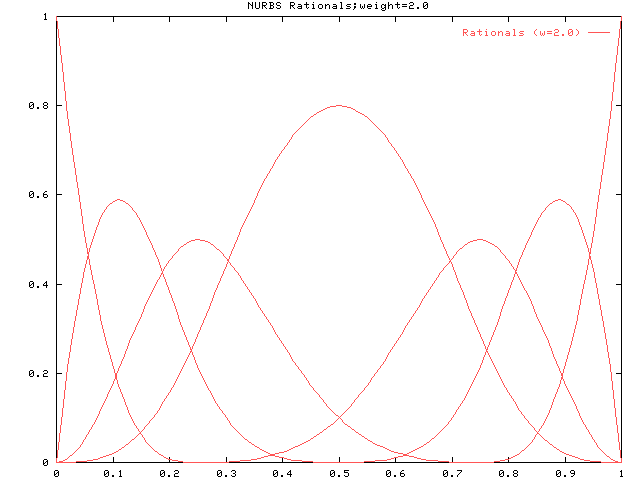
続いてウェイトを0.5にした場合です。 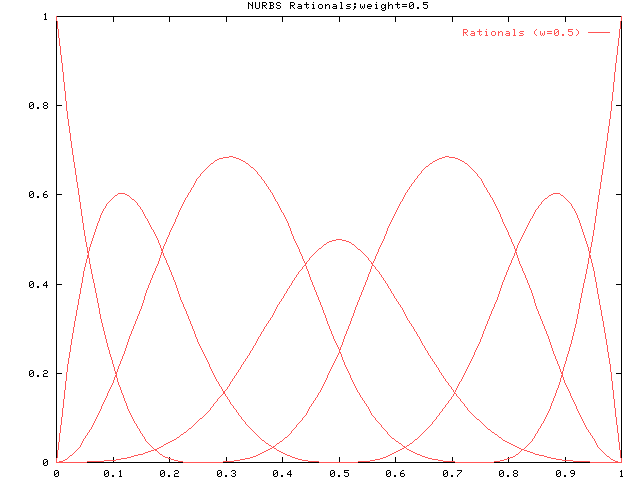
最後にウェイトを0にした場合です。 
下図は上記の有理基底関数を重ねて比較したものです。 p=2と比べて影響範囲が広がっていることがわかります。 これは中央の山が存在する範囲に対応していて、その範囲が広がっているからです。 つまり、次数が上がると1つのウェイトの影響範囲が広がります。 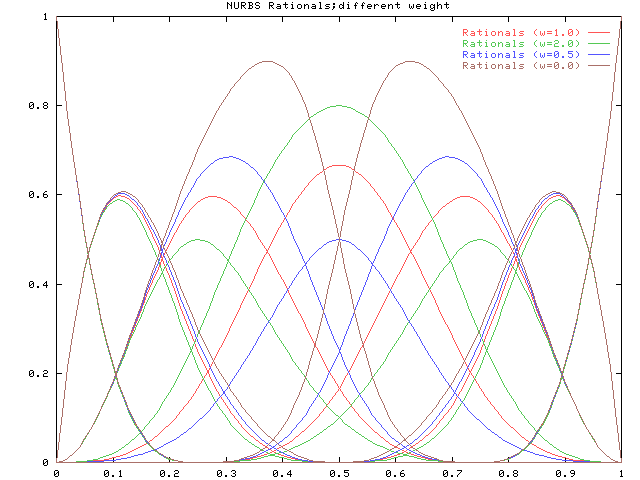
ウェイトを変化させたときの曲線の様子です。 ウェイトが大きくなると曲線は対応する制御点に近くなり、 ウェイトが小さくなると制御点から遠くなる点は同様ですが、 その変化の範囲が広がっていることがわかります。 
曲線の性質:ノットここではノットの性質について示します。 まず多重ノットについてです。 p=2のとき、端点以外のノットを2重にするとその位置で端点のようなふるまいをします。 基底関数の値が1に達しているので、この位置で曲線上の点が制御点に一致することになります。 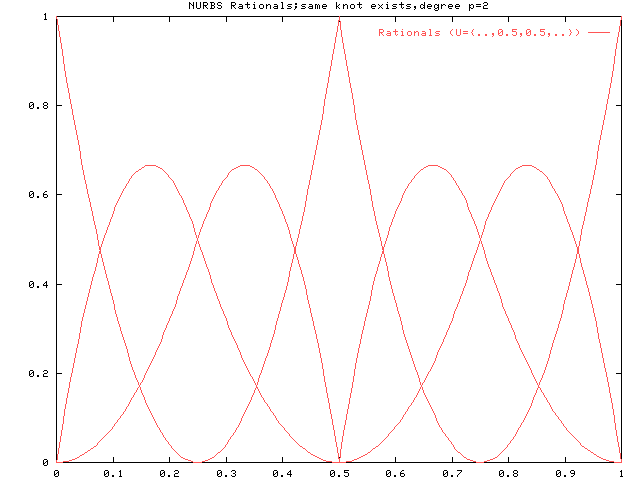
p=3のときは、ノットを3重にすると端点のようになります。 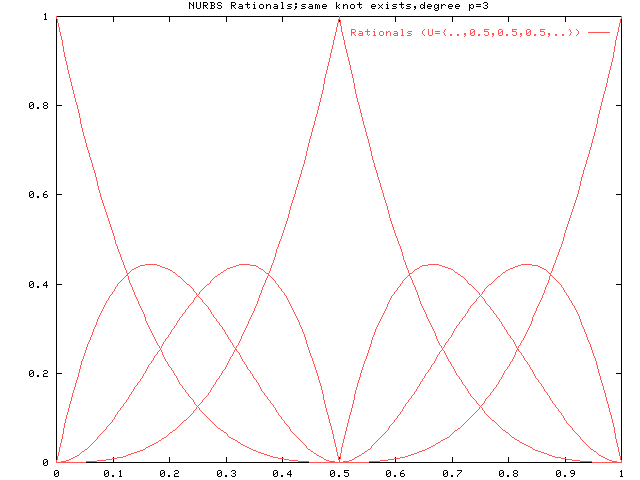
下図は上記を重ねたものです。 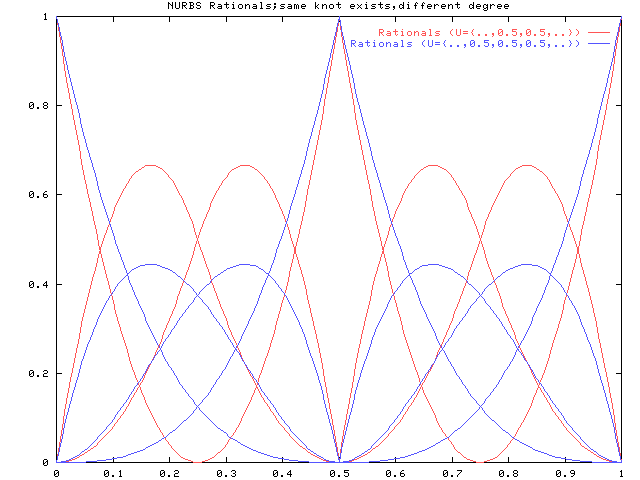
そのときの曲線の様子です。 
次にノット区間幅の変化についてです。 ノット区間幅の変化は、有理基底関数の形を大きく変化させます。 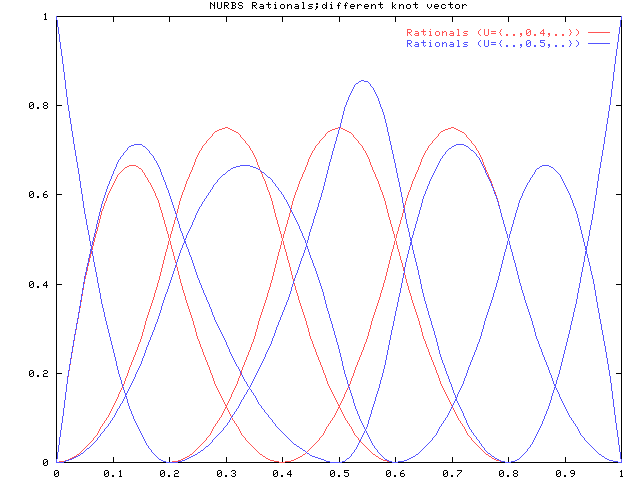
そのときの曲線の様子です。 ノット区間幅の変化では、傾向として区間幅の変化が曲線のセグメント長さの変化として表れますが、 影響範囲が広いので思い通りに変化させることは難しいようです。 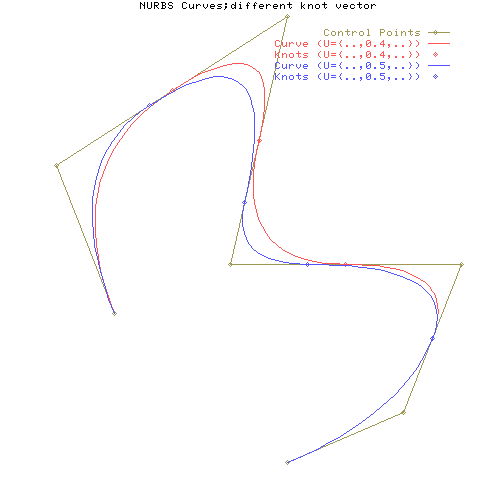
最終更新日 2012-09-24
|