メモリ・ベースト制御による二足歩行の安定化
臨機応変の足運び: 多重軌道間推移による二足歩行制御
二足歩行は高難度の不整地対応の潜在能力が期待されている。
ここで言う不整地とは、絨毯、布団、砂利道、草地、岩場、泥濘、雪、等々を指し、接地状態の予測・事前の運動計画が難しい路面一般を対象としている。
そのため、(1)接地状態に大きく左右されない手法が重要であり、また、(2)その時の状態変化に応じて動く、即応性が重要である。
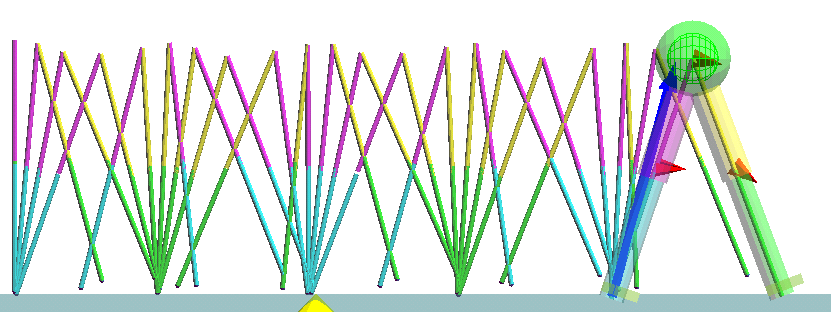
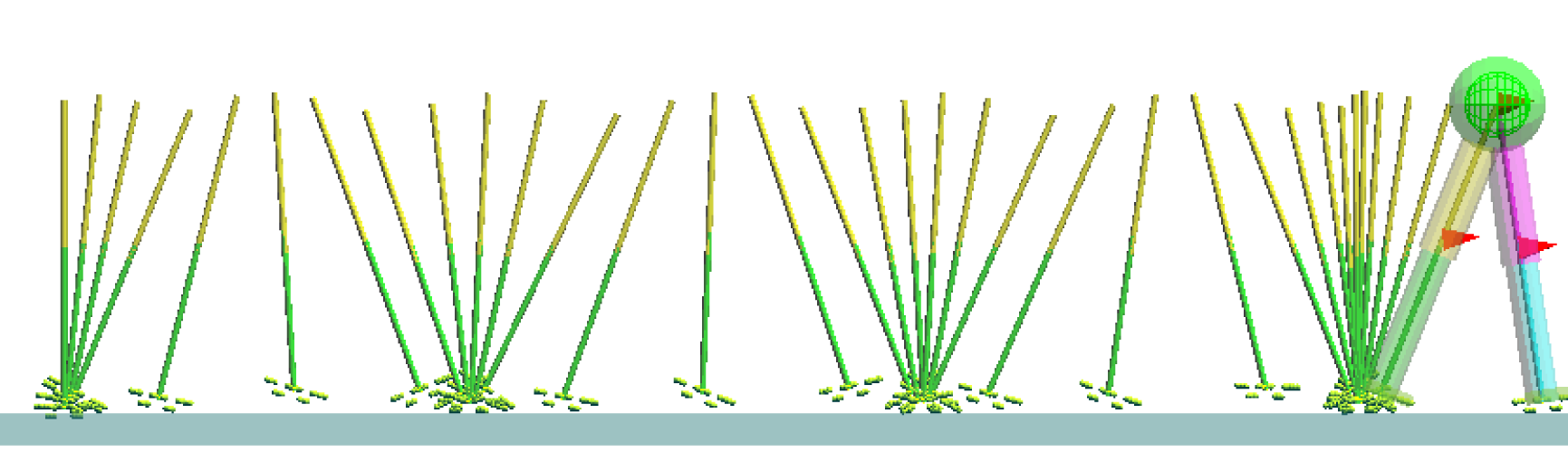
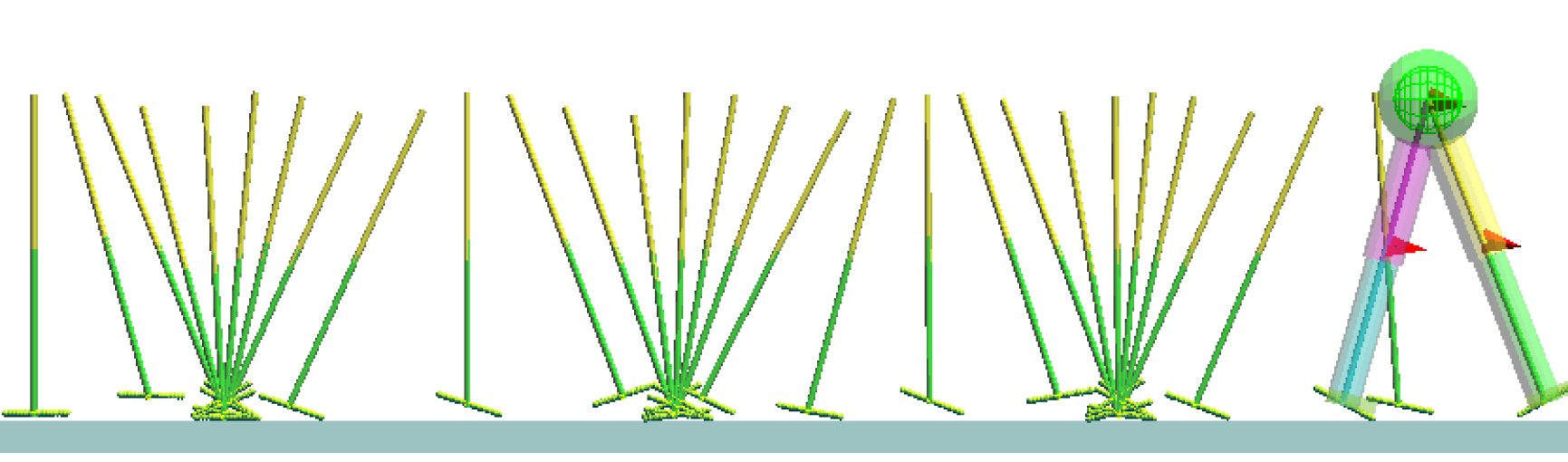
そこで、関係する要因を減らすために、モデルを必要最小限に簡素化した。地面と足先の間は点接地の形に抽象化し、全体を倒立振子(支持脚)と振子(遊脚)の複合振り子と見なした。また、運動は2次元平面内とした。

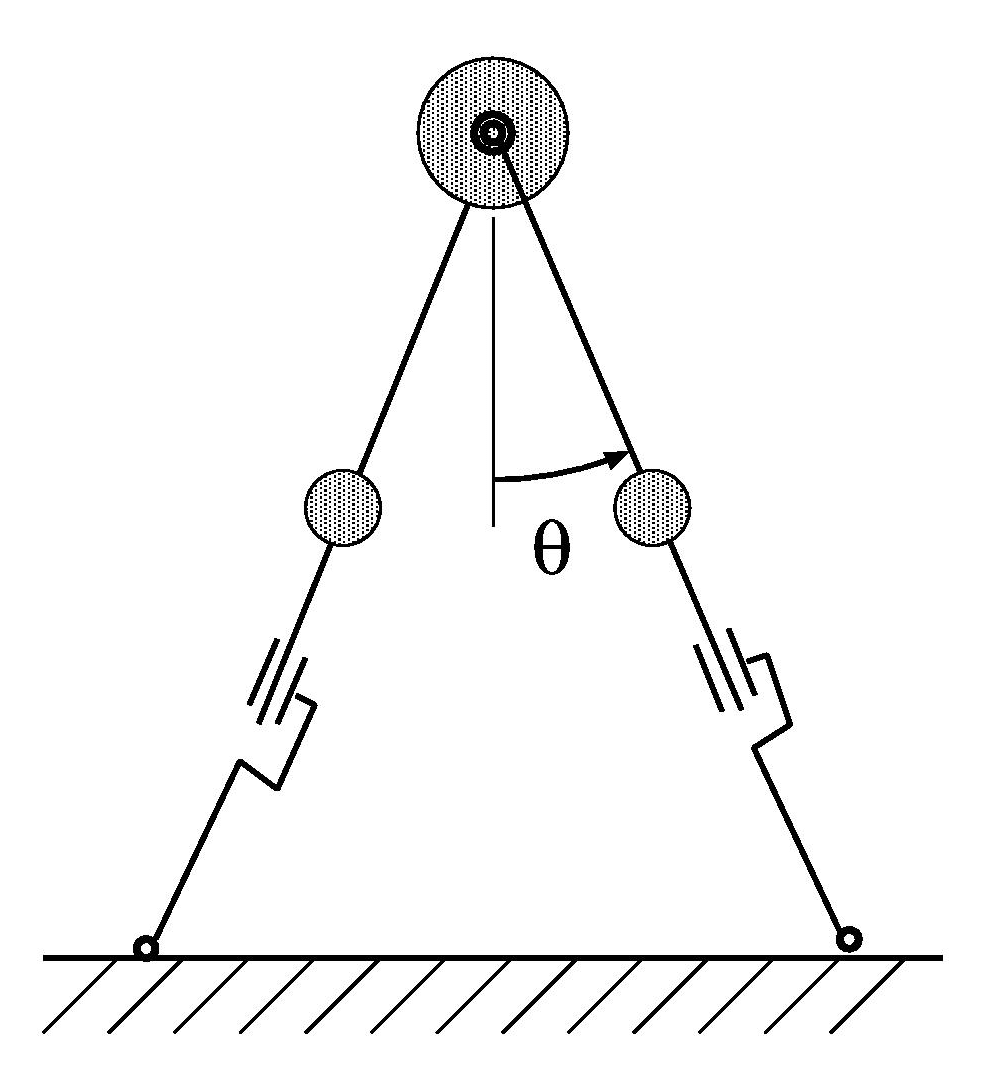
コンパス状2足歩行モデル
このモデルにおいて、転倒の発生は、2つのパタンに集約される。 (1)つまずく=上体に足が着いていかない→転倒 (2)ひっくり返る=上体をおいて足だけ先に行く→転倒 である。つまり、転倒しないためには、上体(全重心)と足先(接地点)との間の位置・速度関係を適切に保つ事が必要である。
制御には2段階を踏む。 (1)うまく歩ける歩行パタンのメモリ作成と (2)メモリ参照による制御である。
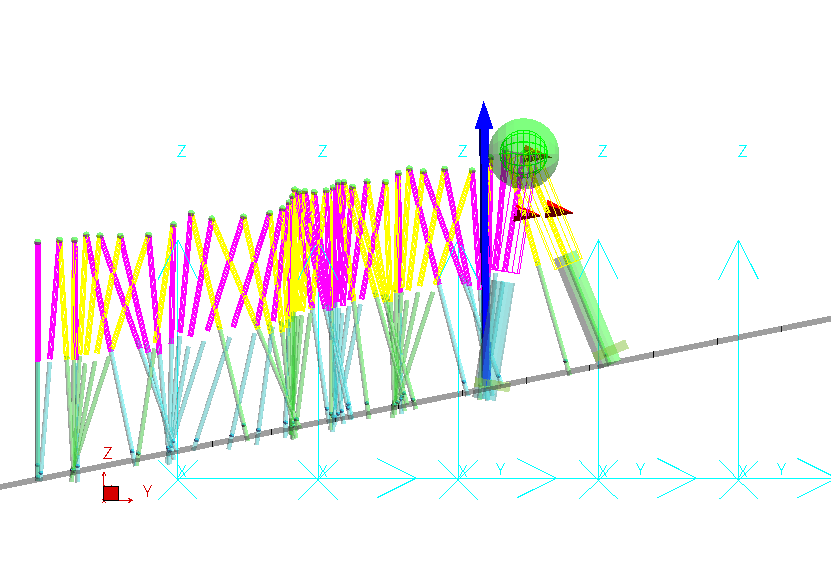
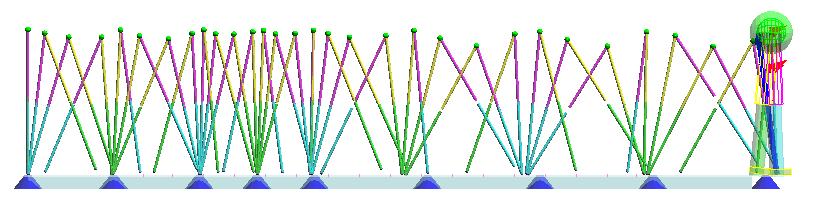
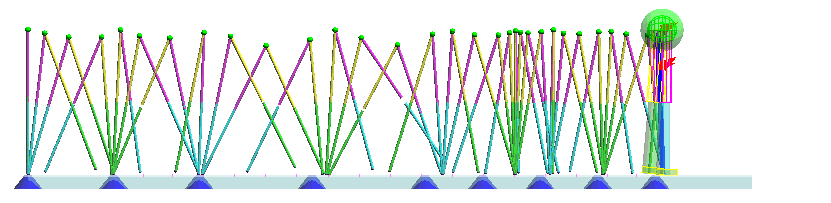
(1)種々の歩調・歩幅での稠密な軌道ライブラリを事前に作成しておく。

様々な歩行パタンでのメモリ生成の段階
歩幅・歩調のパラメータの組(股関節の運動目標値)とそれに対する支持脚(重心と接地点の関係を近似)の軌道(状態変化の軌跡)を対応づけて、保存しておく。
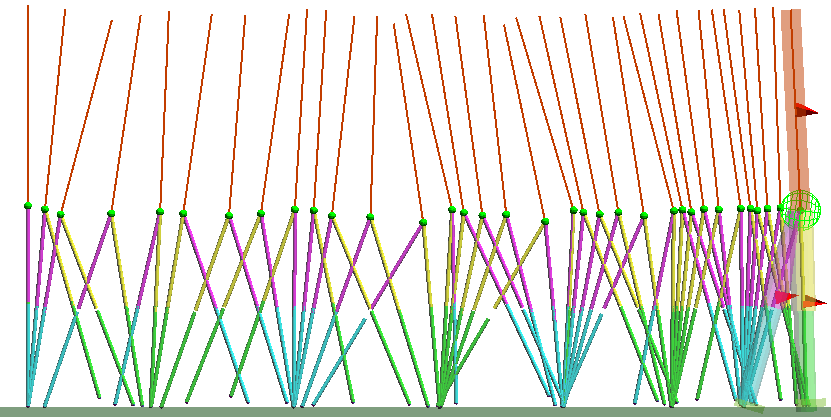
(2)測定した状態をキーにして、参照しながら動作生成を行う。
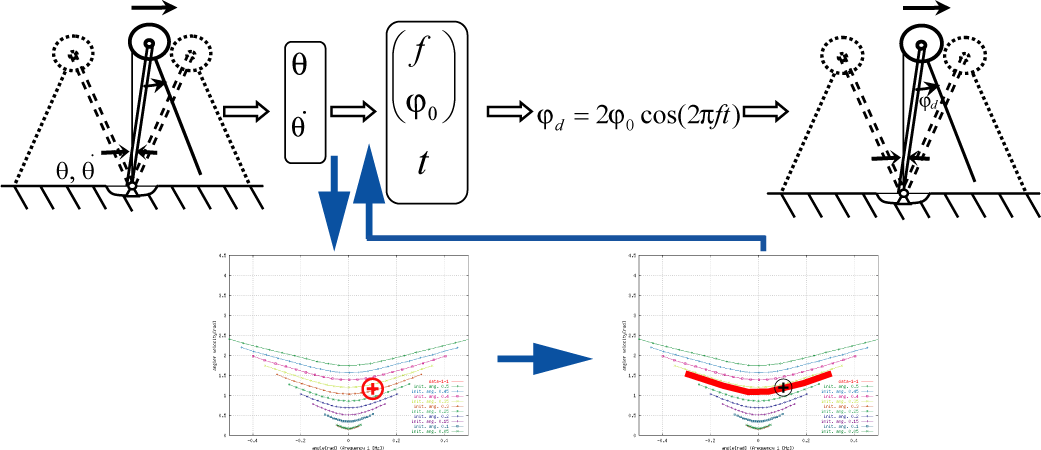
メモリ参照による歩行制御の段階
サンプリング・タイム毎に、その時の支持脚の状態量をキーにして、対応する歩幅・歩調のパラメータの組を引き出す。そのパラメータを股関節の運動目標値にして、制御を行う(運動を再現する)。うまく行った動作のメモリの再現なので、同様にうまく運動生成・制御が行える事が期待できる。
定常的歩行。歩幅の目標値は、股関節角度にして0.6[rad]。
歩行中、外乱が加わっても、足の運びを変えて、歩行バランスを維持し続ける。

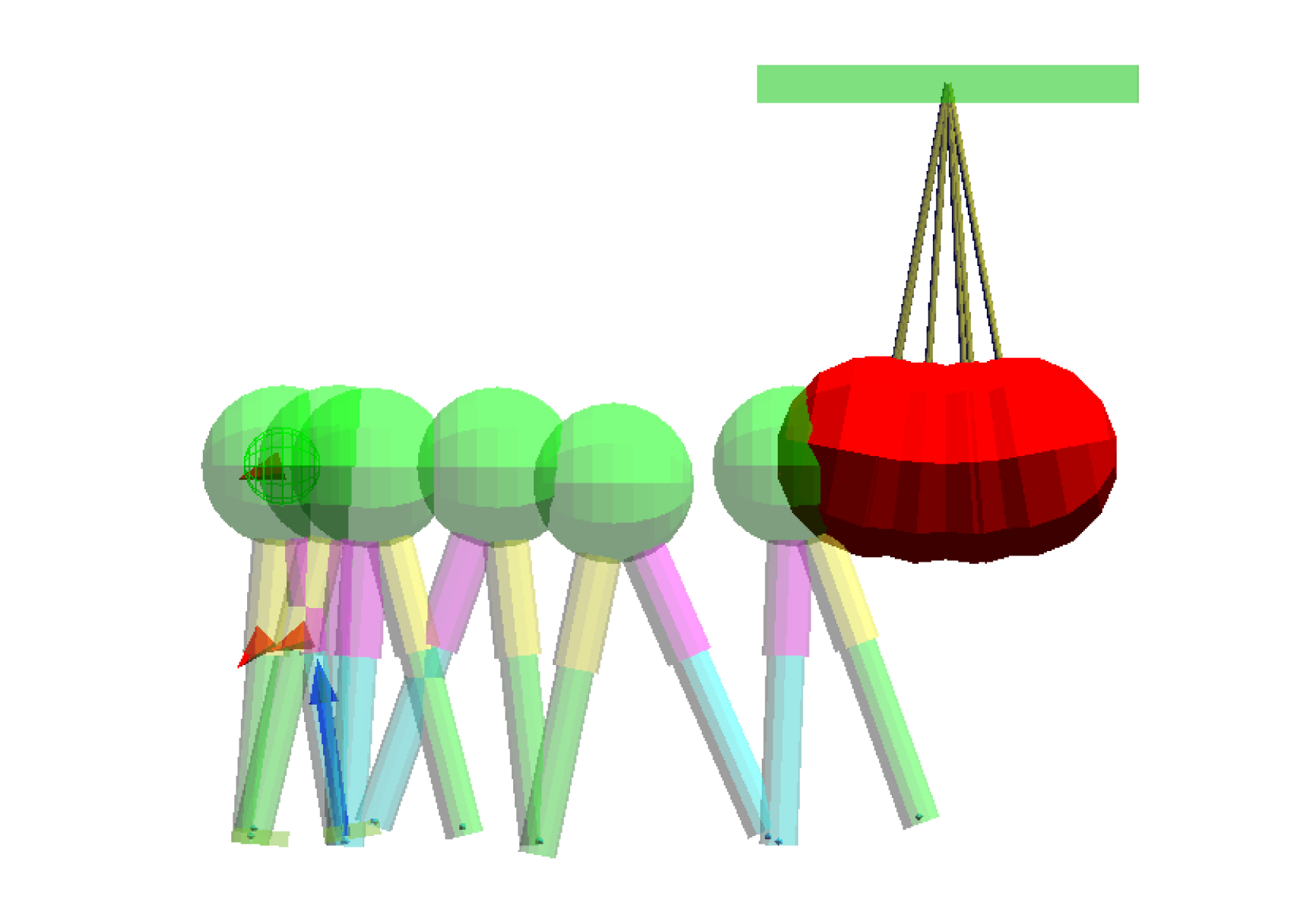
右方向への移動中(左)、大きな外乱(80[kg])が加わり、後ずさりする(右)。 [mp4:0.55MB]

横揺れ地震状態(周波数3[Hz]、振幅5[cm])の路面上の歩行 [mp4:1.7MB]
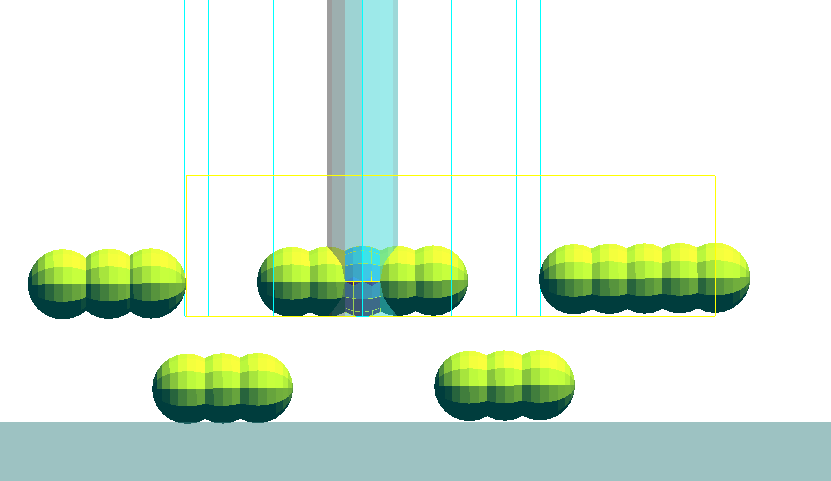
不整地上の歩行。 地面は乱数による折れ線で生成。制御点の振幅は5[cm](最大振れ幅10[cm])。
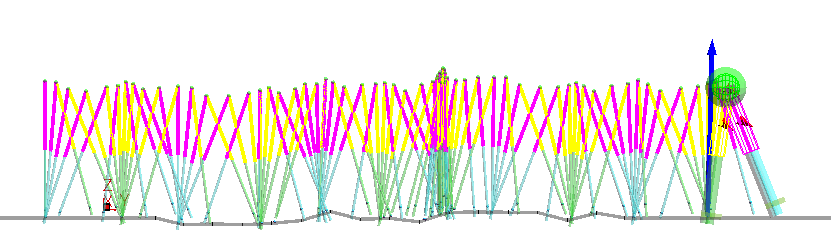
不整地生成用の一様乱数の種が10の場合の歩行 [mp4:0.65--1.2MB]
不整地生成用の一様乱数の種が 1, 2, 3, 4, 5, 6, 7, 8, 9 の場合の歩行。
様々な身体パラメータでの歩行。標準は、上体質量40[kg]、脚自然長1[m]。
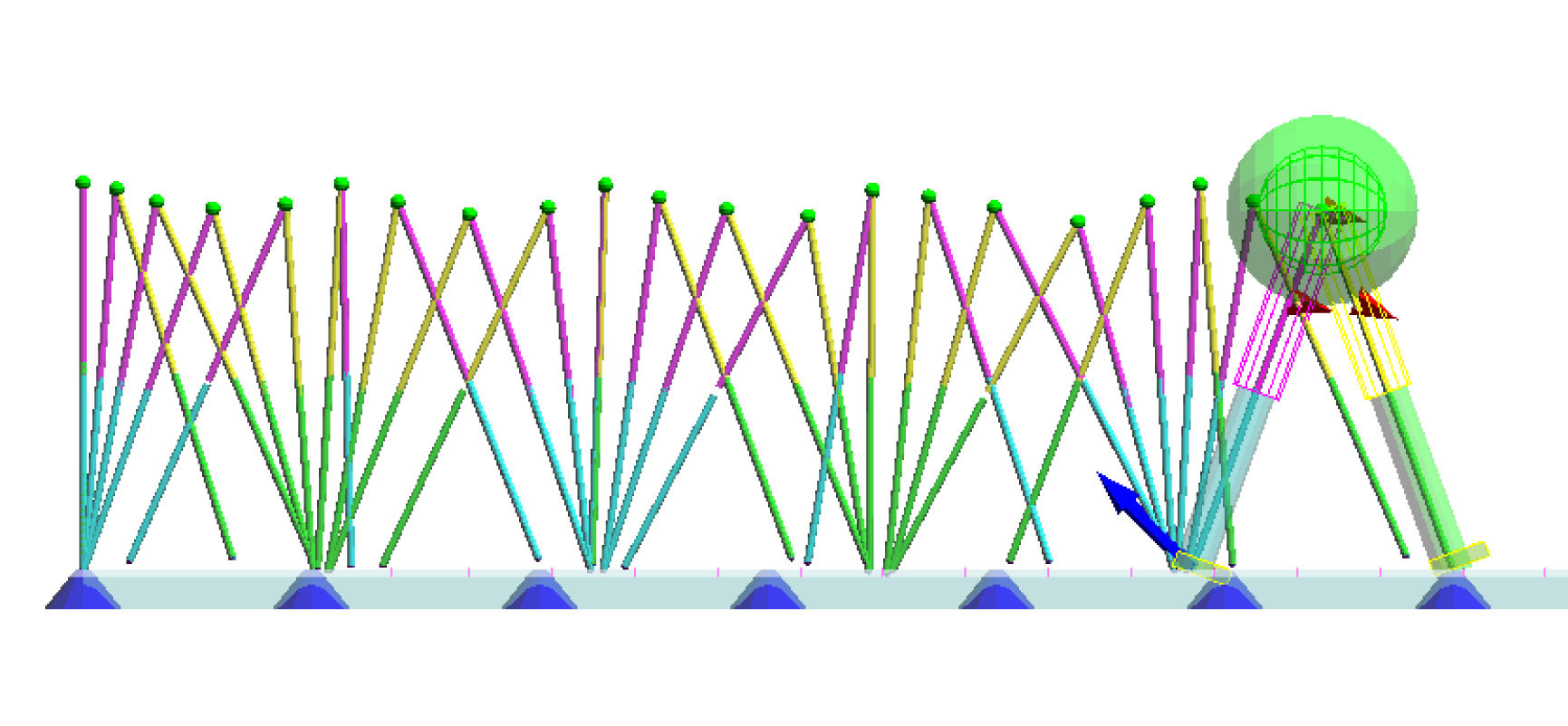
上体の質量を110[kg]まで増量した場合の歩行 [mp4:0.78MB]

上体の質量を20[kg]まで減量した場合の歩行 [mp4:0.56MB]
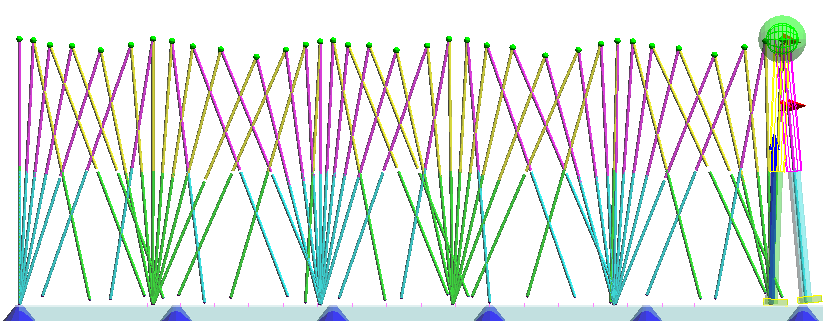
脚自然長を1.65[m]まで伸長した場合の歩行 [mp4:0.73MB]
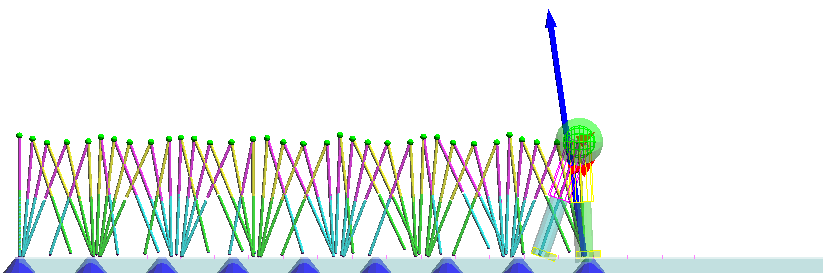
脚自然長を0.75[m]まで短縮した場合の歩行 [mp4:0.57MB]
脚(膝関節)構造を直動型から回転型へと変換。制御のための運動モデルは直動のまま。
上体の構造を点形状から棒状に変更。制御のための運動モデルは、上体が質点のまま。
様々な足裏形状での歩行。踵接地・爪先離地の歩行パタン。蹴り出しの強さは、それぞれの足裏形状に応じて調整してある。図は蹴り出しが小さくて済む順番に並べてある。

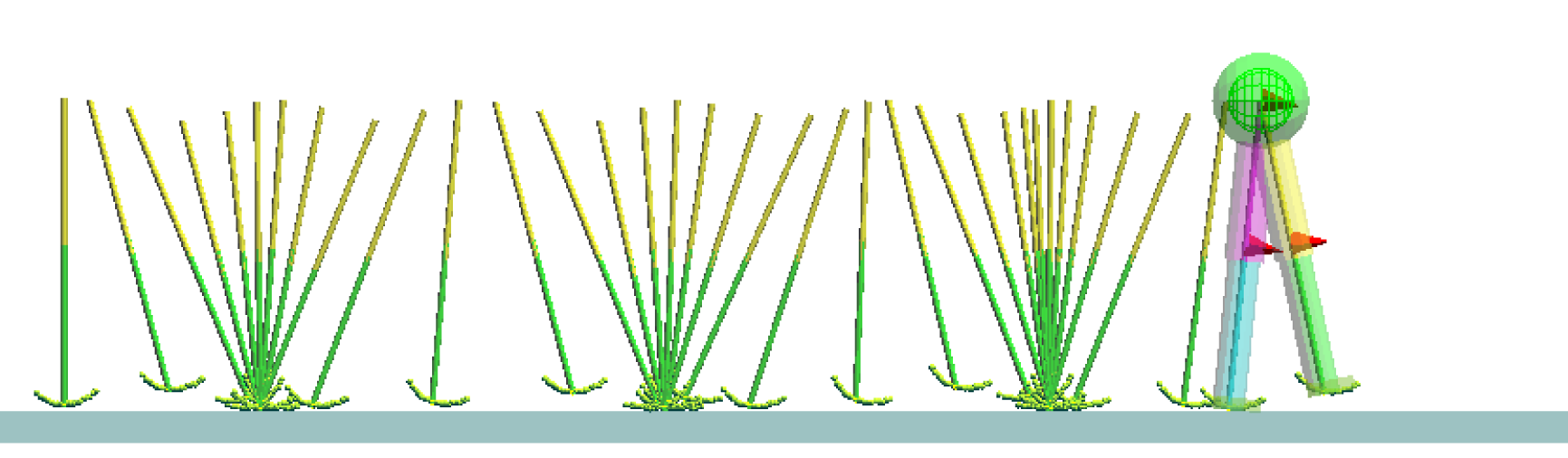
滑らかで歩きやすい形状の足裏での歩行 [mp4:0.44MB]
歩幅の一時的変更による障害物回避。標準の歩幅は、上記の0.6[rad]。

歩幅を一時的に広げた(0.9[rad])場合の歩行 [mp4:0.58MB]

歩幅を一時的に狭めた(0.3[rad])場合の歩行 [mp4:0.58MB]
研究中。床の摩擦係数が小さいところで滑って転倒。