One effective way to verify security protocols is to model them as first-order logic formulas and to use theorem-proving techniques to look for an attack, the absence of attacks being a proof of security. However, it sometimes happens that security proofs cannot be exhibited for correct protocols because of false alarms: this is the problem that we address in [1].
[1] introduces a way to verify secrecy in security protocols modeled as first-order logic formulas that avoids false attacks. The basic idea is to use "rigid variables" to model data that the attacker can instantiate only once and to perform verification for a bounded number of sessions. [1] proposes a complete and terminating decision procedure and the present webpage is about an attempt to implement it.
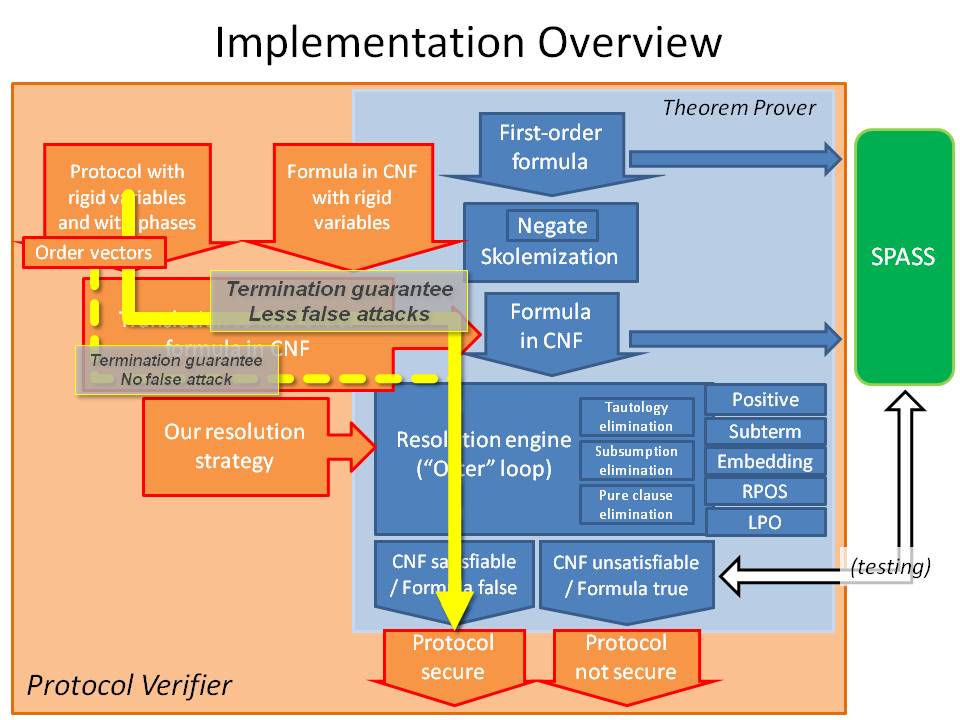
The decision procedure in [1] can be implemented on top of a resolution-based theorem prover by modifying the resolution rule. We have implemented a small theorem prover for this purpose. The transformation to Clause Normal Forms is the naive procedure described in [5] and the resolution loop is the one described in the first part of [6]. The implementation reuses code snippets from [2] and [3]. The resulting implementation has been checked against SPASS [9] using in particular many formulas borrowed from [8]. This theorem prover is equipped with the resolution rule described in [1] and can be fed with models of security protocols using rigid variables through the translation described in [1]. The resulting architecture is summarized on Figure 1.
Our protocol verifier recovers known results for a dozen of protocols and, as expected, succeeds in proving security in some special cases when similar tools fail. The table of Figure 2 summarizes the results. The property verified is always a secrecy property. For each protocol, the number of parallel sessions and successive phases is displayed (there is only one session or phase when not stated otherwise), the number of rigid variables (the total number is for all the sessions), the number of input clauses and worked off clauses (see [6] for terminology), and the running time. Benchmarks show that the protocol verifier is sound but performance degrades rapidly with the number of rigid variables.
| A -> B | : | [A,N0]KAB |
| B -> A | : | [B,N0,N1]KAB, [B,N0,N2]KAB |
| A -> B | : | N1 |
| Figure 3 |
Let us consider the running example of [1] (sample_protocol in Figure 2). Let [M]K be the encryption of M with the symmetric key K. Relying on the long-term shared secret key KAB, A wants to establish a short-term secret with B. B generates two nonces N1, N2 and sends them separately. A acknowledges both nonces by sending back one of them. The short-term secret is N1(+)N2. The protocol in Alice-and-Bob notation is displayed in Figure 3.
In our prototype, the protocol of Figure 3 is basically written as follows (Figure 4):
| <A,0> | -> I[senc{pair{%A,%N0},%KAB}] , |
| <B,0> | I[senc{pair{%A,@x},%KAB}] -> I[pair{senc{triple{%B,@x,%N1},%KAB},senc{triple{%B,@x,%N2},%KAB}}] , |
| <A,1> | I[pair{senc{triple{%B,%N0,@y},%KAB},senc{triple{%B,%N0,@z},%KAB}}] -> I[@y] |
Figure 4 |
Each rule is prefixed the the agent id and the step number; @'s are for rigid variables; %'s are session-specific place-holders. It remains to specify the intruder capabilities (see Figure 5(a) for the Dolev-Yao intruder with symmetric keys), the data for session-specific place-holders (see bottom of Figure 5(a) and top of Figure 5(b)), data known by the intruder such as corrupted keys and nonces (see Figure 5(b)), and the goal (see last part Figure 5(b)).
The executable works by first translating a protocol specification (such as the one of Figure 5)
into a first-order logic formula preserving satisfiability (option -proto) and
then checking satisfiability using the decision procedure of [1] (option -satis), e.g.:
$ ../rigid -proto -file sample_protocol.rig | ../rigid -satis ours -time -stdin
2 roles; 1 phases; 6 sessions; 3 rigid variables (total: 18)
32 input clauses
saturation, input cnf satisfiable: 0 us. cl.; 192 wo. cl.
processor time used by resolution: 2.184137
Here are all the options (warning: the option -proto_order is not yet fonctional!):
$ ../rigid --help
Usage: ../rigid [options]
-verb verbose mode
-debug debug mode
-time elapsed processor time
-file input file
-stdin use standard input as input file
-sub test subsumption
-sublin test linear subsumption
-lpo test lpo
-spass_fo translate a closed first-order formula into SPASS syntax
-spass_cnf turn a set of clauses into SPASS syntax
-prove try to refute the negation of a formula
-satis check satisfiability of a cnf
-trans translate rigid variables to flexible ones in a cnf, preserving satisfiability
-proto translate a protocol spec. into 1st-order clauses, preserving satisfiability
-proto_order same as -trans with order vectors
-help Display this list of options
--help Display this list of options
The current implementation only avoid false alarms due to replaying of rules. It remains to extend the implementation so as to avoid all false alarms (as explained in [1]).
First time online: March 31, 2009.
Contact information: Reynald Affeldt (reynald dot affeldt at aist dot go dot jp)