岩石磁気の基礎の基礎　その1

産総研
last updated 2023.9.22
地磁気は記録される
（綱川秀夫著『地磁気逆転X年』（岩波ジュニア文庫）より）
  • 岩石に磁性を示す鉱物が含まれている
  • これらは地磁気と同じ方向に磁化する
  • 都合がよいことに、一度磁化してしまうとまわりの地磁気が変わっても動じない
  • ただし、磁化は小さい
岩石の磁気から知りたいこと（例）
  • 測定対象とした岩石ができたときの地球磁場の方向から、岩石のできた場所を復元する
  • 昔の地球磁場の強さを推定する
  • 磁性鉱物がたまった環境を復元する
  • 磁性鉱物ができる環境を推定する
  • 磁性鉱物を化石のように使って層序を復元する
基礎的な定義
    　　　　
  • 『古地磁気学』（Robert F. Butler 著　渋谷秀敏訳）より
    　　　　
    　　　　
  • 磁気モーメントM
    • 磁気双極子モーメント、簡単には磁気モーメントM は、一対の磁荷としても一つの環状電流としても定義できる。
      一対の磁荷として定義するなら、磁荷の大きさをm 、正負二つの磁荷を距てる無限小の距離ベクトルをl 、とすると、磁気モーメントM は
      M = ml
      で与えられる。
    • 一方、環状電流として定義するなら、環の面積をA 、電流をI とすると、
      M = IAn
      となる。
    • ここで、n は環と垂直な単位ベクトルである。n の方向、したがってM の方向、は右手の法則によって与えられる。 すなわち、電流の方向に右手の親指以外を巻いたときに親指の方向がn の方向になる。
      環電流で磁気モーメントを定義するのは、磁気モーメントはすべて電流によっているのであるから、より基本的である。
      しかし、磁気モーメントが磁荷の対からなっていると考えた方が便利なこともある。
  • 磁場H
    • ある領域の磁力場ないしは磁場Hはそこに置いた正の単位磁荷が受ける力として定義できる。 実行可能な実験は、磁場中に置いた磁気モーメントが磁場に揃おうとするトルクを観察することだろう。
    • このトルクΓ はベクトル積(外積) を用いて
      Γ =M×H = MHsin θΓ
      で表される。
      ここで、θ はM とH のなす角の大きさ、Γ はΓ方向の単位ベクトルである。
    • 自由に回転できる磁気モーメントは磁場の方向に揃う。方位磁石の針は磁気モーメントを持っていて、 地球磁場の水平成分の方向を向くようになっている。それで、磁気方位角を決定できるのである。
      磁場中での磁気モーメントの方位のエネルギーはこれから岩石磁気学の勉強が進むとしばしば出てくる。
      この位置エネルギーはベクトルのスカラー積を用いて、
      E =ーM・H =－MHcosθ
      で表される。
      記号が負となっているのはM とH が平行になったときにエネルギーが最小になることを表している。

  • 磁化Jと帯磁率（磁化率）χ

    • ある物質の磁石の強さあるいは磁化J は単位体積あたりの磁気モーメントの量である。
    • ある体積の磁化の大きさを計算するには、磁気モーメントのベクトル和を体積で割ればいい。
      J =ΣMi／体積
      Mi というのは構成している磁気モーメントである。
    • 磁化の強さの単位はＴ（テスラ）またはWb/m2
    • 磁化は誘導磁化と自発磁化の二つに分類できる。
      ある物質が磁場H にさらされると、誘導磁化Ji が生じる。
      生じる磁化と磁場は帯磁率（磁化率）χで結びつけられる。
      Ji = χH
      つまり、帯磁率（磁化率）χ はある物質の磁化しやすさと見ることができる。
    • 上の式では帯磁率（磁化率）χとしてスカラーを取った。これは磁化と磁場が平行となることを暗黙に仮定していることとなる。
      しかしながら、磁気異方性を示す物質もある。そのような物質ではJi はH と平行にはならない。
      磁気異方性を持った物質では、x 方向に磁場をかけても一般にはx 方向だけではなくy, z 方向の磁化も生ずる。
      この様な場合は、帯磁率（磁化率）は3×3 の行列で表されるようなテンソルとなる。
    • 現在の磁場の働きかけの結果である誘導磁化に加えて、残留磁化Jr を持つ物質もある。
      残留磁化はその物質に働いた過去の磁場を記録している。
    　　　　
  • 物質の磁性（山部恵造著『磁石のふしぎ磁場のなぞ』（けやき出版）と近角聡信著『強磁性体の物理』（裳華房）より）
  • 物質の磁性とは
    • 磁場の中に置かれたとき、その物質がどんなふうに動くかということである。
      わずかではあるが磁場の方向に磁化されるものを常磁性、逆方向に磁化されるものを反磁性という。
      この場合、反応の強さ（磁化の大きさ）は磁場の強さに比例する。この比例定数を磁化率または帯磁率という。
    • 磁石に強く引き付けられるものには、強磁性（ferromagnetism）とフェリ磁性（ferrimagnetism）がある。
      • 強磁性 (Ferromagnetism) とは、隣り合うスピンが同一の方向を向いて整列し、全体として大きな磁気モーメントを持つ物質の磁性を指す。
        そのため、物質は外部磁場が無くても自発磁化を持つことが出来る。
        室温で強磁性を示す単体の物質は少なく、鉄、コバルト、ニッケル、などである。
        単に強磁性と言うとフェリ磁性を含めることもあるが、日本語ではフェリ磁性を含まない狭義の強磁性をフェロ磁性と呼んで区別することがある。
      • フェリ磁性 (Ferrimagnetism) 体とは内部に強磁性体と反強磁性体の部分をあわせ持つ磁性体である。
        酸化物の磁性体でフェライトと呼ばれるFeO･Fe2O3、MnO･Fe2O3、NiO･Fe2O3、CoO･Fe2O3が代表である。


    • 反磁性（diamagnetism）

      • 反磁性とは、物質がいわゆる磁性原子を含まないような場合に現れる非常に弱い磁性で、
        磁化率は負となり、その値は10-5程度である。
        反磁性は有機化合物などによくみられる。
        反磁性磁化率は温度によってあまり変化しない。
    • 常磁性（paramagnetism）
      • 常磁性とは、外部磁場が無いときには磁化を持たず、磁場をかけるとその方向に弱く磁化する磁性を指す。
        磁化率は正となりχ＝10-5～10-2程度である。
        常磁性の物質の磁化率（帯磁率）χは絶対温度に逆比例する。これをキュリーの法則と呼ぶ。
        χ＝Ｃ／Ｔ
        比例定数Cはキュリー定数と呼ばれる。
  • キュリー温度とネール温度
    • 常温では強磁性や反強磁性を示す物質が、ある温度以上になると、スピンは互いにでたらめの方向を向くようになって常磁性を示すようになる。
      この温度を強磁性ではキュリー温度、反強磁性ではネール温度という。
  • フェルベー点（Verwey transition）
    • Fe－フェライトは磁鉄鉱（magnetite）と呼ばれ、人類が発見した最も古い磁性体である。
    • スピネル格子で、単位胞の中に32個のO2-イオンと8個のAイオンと16個のBイオンの計56個のイオンを含む。
    • 磁鉄鉱はBイオンにFe3+とFe2+が同居するため、それらの間を電子が飛び移るホッピング伝導を行う。
      そのため、フェライトの中では異例に電気抵抗率が低い。
      125Kでこのホッピングは停止し、その温度以下で電気抵抗は急上昇し、結晶がひずむ。
      この変態点をフェルベー点という。

      http://www.ne.jp/asahi/iwamizawa/baraken/Crystal-model/Crys-FeO/Fe-FeO3.htm

      実は、フェルベー相変態(Tv)の起きる理由は、まだ完全には解明されていないらしい。
    • 自然物のマグネタイトのフェルベー点は110-120K。

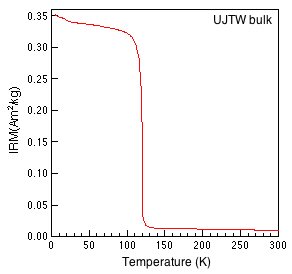
      2008年7月: 鳥居雅之, J-DESCコアスクール・古地磁気コースの講習資料「MPMSによる低温磁気測定」より

    • 粒径、酸化度によってTvの現れ方が変わる。低温酸化されるにしたがってTvが低温側にシフトする。（Ozdemir et al.,1993)

    • 純粋なマグネタイトではなく、ウルボスピネルとの固溶体を作っているチタノマグネタイトになると、Tvの現れ方はさらに複雑（Moskowitz et al., 1998）。

    • MPMSによる低温磁気測定が広く行われるようになって、古地磁気研究でも注目されている。

      とりわけ、堆積物などの変質しやすい試料の研究方法として優れている。
      室温以下の低温での測定の大きな利点は、加熱しないので、試料の酸化や熱による変質が起こらない。
      この点が、同じく温度に対する磁性の変化を測定する高温測定との大きな違い。
      とくに典型的な研究例として、ODPの堆積物中の磁性鉱物が、海底直下の酸化的な環境から深度とともに還元的になるしたがって変化していく 例がある(Torii, 1997)。

  • モーリン点（Morin transition）
    • ヘマタイト（α-Fe2O3）は低温（250K以下）ではｃ軸方面に磁化を持つ反強磁性であるが、 高温（250-963K）ではｃ面に磁化を持つ傾角磁性になる。この250Kの転移点をモーリン点という。
　　　　
ここでおさらい

その１！

2つの磁極の強さをm1（Wb)、m2(Wb)とし、2極間の距離をr(m)とすれば、その間に働く力F(N)は
F=m1m2/(4πμ0r2）
ここに真空の透磁率μ0＝4π×10-7（H/m）
H(ヘンリー）＝Wb/A
磁場の強さはA/mで表す。

磁場Hの存在している場所にm(Wb)の磁極を持ってくると磁極には力Fが働き
F=mH(N)
今、+m、-mの2極を持つ、長さｌの棒磁石を磁場Hの中に入れると力が作用して偶力のモーメントを形成する。
L=-mlHsinθ　(Nm)

ここで磁石に対するどんな力を考えてもmとlは常に積の形で現れるので、この積を磁気モーメントと呼ぶ。
M=ml(Wbm)
磁性体の磁化Jは単位体積中の磁気モーメントの和である。
J=ΣM／体積　よって単位はWbm/m3＝Wb/m2＝T

その２！

電磁誘導から磁化を測定すると
コイルの断面積をS(m2)、巻き数をNとしたときの起電力はV=-NS(dB/dt)となる。

このBは磁束密度（T=Wb/m2）と呼ばれる量で磁化Jと磁場Hとの関係は
B=J＋μ0H
　 J=χHであるときは
B=(χ+μ0）H
B=μH
μを（体積）透磁率（permeability）という。

ちょっと混乱してきた

磁性では単位系がごちゃごちゃになってくる。
それはE-H対応系とE-B対応系があるからだという。
電場Eに対応するものをHにするかBにするかの違いだが、注意を要する。

  • E-H系は、磁気双極子モーメントを考え、それらに働く力から磁場（H）を定義し、
    磁場中に置かれた物質の磁化（J：単位体積当たりの磁気モーメント）と磁場から磁束密度（B）を定義する。
    すなわち
    B=J＋μ0H

    　
  • E-B系は電流または運動する電荷（e）に働く力（F：ローレンツ力）から直接磁束密度（B）を定義する。
    すなわち
    F=ev×B
    ｖは電荷の速度
    磁場はH=B/μ0
    E-B系ではHを磁場の強さ、Bを磁場と呼ぶことが多い。

注意すべき磁気量

  • 磁化は

    E-H系では、J=B-μ0HだからWb/m2＝T
    磁束密度（B）と同じ単位になる。
    E-B系では、M=(B/μ0）-Hで、A/m
    磁場（H）と同じ単位になる。
    E-H系の磁化JはE-B系では磁気分極Jと呼ばれる。

  • 磁気モーメントは

    E-H系では磁気双極子モーメントを考え、Wbmを使う。
    E-B系では円環電流によるものを考え、Am2を使う。

  • 磁場は

    E-H系ではH(A/m）、E-B系ではB（T)を磁場と呼ぶ。

    物理量が違うので注意を要する。

  • cgs-emu系（長らくこの体系で考えられてきた）

    • 磁荷ｍ

      真空中、1cmの距離で1dyneの力を及ぼしあう、等量の磁気量を1cgs-emu単位の磁荷という。

    • 磁場H

      1cgs-emuの磁荷に対して1dyneの力を生じる磁場の強さを1gaussまたは１Oeとする。

    • 磁化J

      棒状物体が磁化され、その両端に+m、-mの磁荷が現れているとき、端面の面積をSとするとJ=m/Sを磁化の強さとし、gaussで表す。

      これは単位体積当たりの磁化の強さであることに注意。

    • 磁束密度B

      磁場に垂直と見なせる断面に現れる単位面積当たりの磁気量を言う。gaussで表す。

  • 単位の換算
    QuantitySIcgsSI×f→cgscgs×f→SI
    Magnetic induction(B)TG1T=1Wbm2×104→G1G×104→1T
    Magnetic field(H)A/mOe1A/m×(4π/103)→Oe1Oe×(103/4π)→A/m
    Magnetic moment（Mv)Am2emu1Am2×103→emu1emu×10-3→Am2
    Volume magnetization（M)A/memu/cc1A/m×10-3→emu/cc1emu/cc×103→A/m
    Mass magnetizationAm2/kgemu/g1Am2/kg×1→emu/g1emu/g/kg×1→Am2
    Bulk susceptibilitym3emu/Oe1m3×(106/4π)→emu/Oe1emu/Oe×(4π/106)→m3
    Volume susceptibility（κ）[SI][G/Oe]1[SI]×(1/4π)→[G/Oe]1[G/Oe]×(4π)→[SI]
    Mass susceptibility（χ）m3/kgemu/(Oe*g)1m3/kg×(103/4π)→emu/(Oe*g)1emu/(Oe*g)×(4π/103)→m3/kg


  • 体積磁化率：κ＝M/H
    H：磁場（A/m）、M：単位体積当たりの磁化（A/m）

  • 質量磁化率：χ＝κ/ρ
    κ：体積磁化率（無次元）、ρ：密度（kg/m3）

  • 磁気ヒステリシス

    コアスクールテキストより

    強磁性体においては、その磁化は加えた磁場に比例せず、ヒステリシスを示す。
    ヒステリシスループの形は磁性体の性質によって違う。
    (0)→(1):初磁化曲線
    (2): 残留磁化:飽和等温残留磁化（SIRM)
    (3): 保磁力
    κ：初生帯磁率
    Hc：保磁力
    Hcr：残留保磁力
    Ms：飽和磁化
    Mrs：飽和残留磁化
  • よく出てくる磁性鉱物(鳥居,2005;AGU,1995)

      MineralFormuraJs(Am2/kg)Tc(℃)Tv(K)Density(103kg/m3)Volumeκ(SI)Massχ(10-3m3/kg)
      マグネタイト（Magnetite)Fe3O490-925801205.181.0-5.70.2-1.1
      ヘマタイト（Hematite)α-Fe2O30.4675～2605.260.0005-0.040.0001-0.0076
      マグヘマイト（Maghemite)γ-Fe2O370-80590-675-4.902.0-2.50.4-0.5
      ゲーサイト（Goethite)α-FeOOH<1120-4.270.0011-0.0120.00026-0.0028
      ピロータイト（Pyrrhotite)Fe7S820320344.623.20.69
      グレイガイト（Greigite)Fe3S4～25-----
      チタノマグネタイト(titanomagnetite)Fe3-xTixO4-※？4.98(x=0.6)0.13-0.62(x=0.6)0.025-0.12(x=0.6)


    • 典型的な岩石の磁化強度と磁化率

    • AGU(1995)より抜粋

      RockDensity(103kg/m3)Volumeκ(SI)Massχ(10-3m3/kg)
      安山岩（Andesite)2.610.170.065
      玄武岩（Basalt)2.990.00025-0.180.000084-0.061
      輝緑岩（Diabase)2.910.001-0.160.00035-0.056
      閃緑岩（Diorite)2.850.00063-0.130.00022-0.044
      斑レイ岩（Gabbro)3.030.001－0.090.00026-0.03
      花崗岩（Granite)2.640-0.050-0.01900
      橄欖岩(Peridotite)3.150.096-0.20.03000-0.062
      流紋岩(Rhyolite)2.520.00025-0.0380.00010-0.015
      蛇紋岩(Serpentinite)2.780.0031-0.0180.0011-0.0063


    • メモ
      • キュリー温度→鉱物の種類によって違う

      • 保磁力→鉱物の種類によって違う（ヘマタイト高い、マグネタイト低い）

      • 保磁力→同じ鉱物でも粒子サイズによって違う（サイズ大は低い、サイズ小は高い）