ここで磁性体は磁化強度J,磁化方向pで一様に磁化している四角柱の組み合わせで近似する.
以下に, Z軸が鉛直下方に向うデカルト座標系を考え,四角柱モデルの原点(x=y=z=0)における全磁力異常を計算するための理論式(Nakatsuka,1981)を表す.
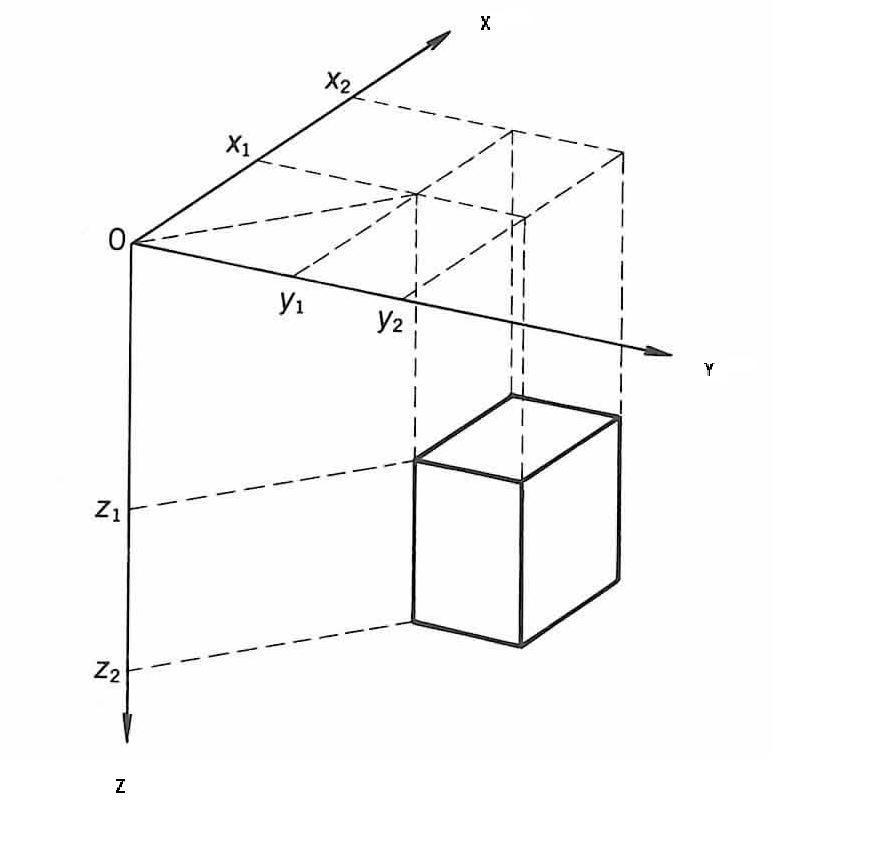
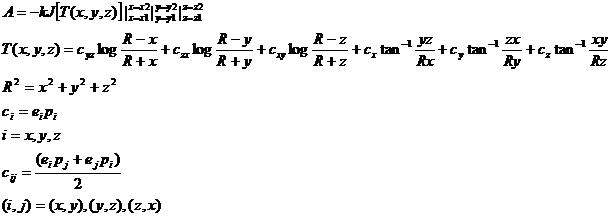
この式は広く知られる理論式(Bhattacharyya,1964)からモデルのサイクリックな性質を保存した表現で,実用的である.
ここで,Jは磁性体の磁化強度, (px,py,pz)は磁化の方向余弦を示す.
また磁気異常は外部磁場に比べて十分に小さいことから,eを地球磁場方向の単位ベクトルとし,方向余弦(ex,ey,ez)を与える.
k(磁化率)はemu系では1,SI系では1/4πとなる.
磁性体の磁化は,理想的には誘導磁化と残留磁化のベクトル和に相当する値を与えることになる.
具体的なモデル設定は以下のように行う.
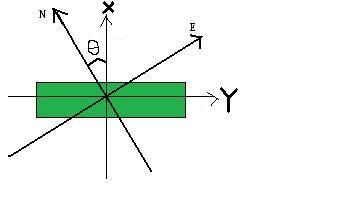
X軸の方位θは北(N)から時計回りに与える。
以下に, Z軸が鉛直下方に向うデカルト座標系を考え,四角柱モデルの原点(x=y=z=0)における全磁力異常を計算するための理論式(Nakatsuka,1981)を表す.

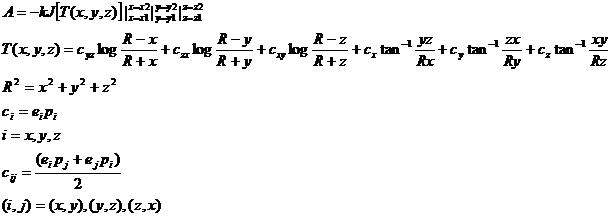
この式は広く知られる理論式(Bhattacharyya,1964)からモデルのサイクリックな性質を保存した表現で,実用的である.
ここで,Jは磁性体の磁化強度, (px,py,pz)は磁化の方向余弦を示す.
また磁気異常は外部磁場に比べて十分に小さいことから,eを地球磁場方向の単位ベクトルとし,方向余弦(ex,ey,ez)を与える.
k(磁化率)はemu系では1,SI系では1/4πとなる.
磁性体の磁化は,理想的には誘導磁化と残留磁化のベクトル和に相当する値を与えることになる.
具体的なモデル設定は以下のように行う.

X軸の方位θは北(N)から時計回りに与える。
- 誘導磁化:J=κH κ:体積磁化率(SIならば無次元),H:外部磁場強度
- 測定値が無い時の目安の例
- Physical Properties of Rocks, G.Angenheister ed., Springer-Verlag, 1982より
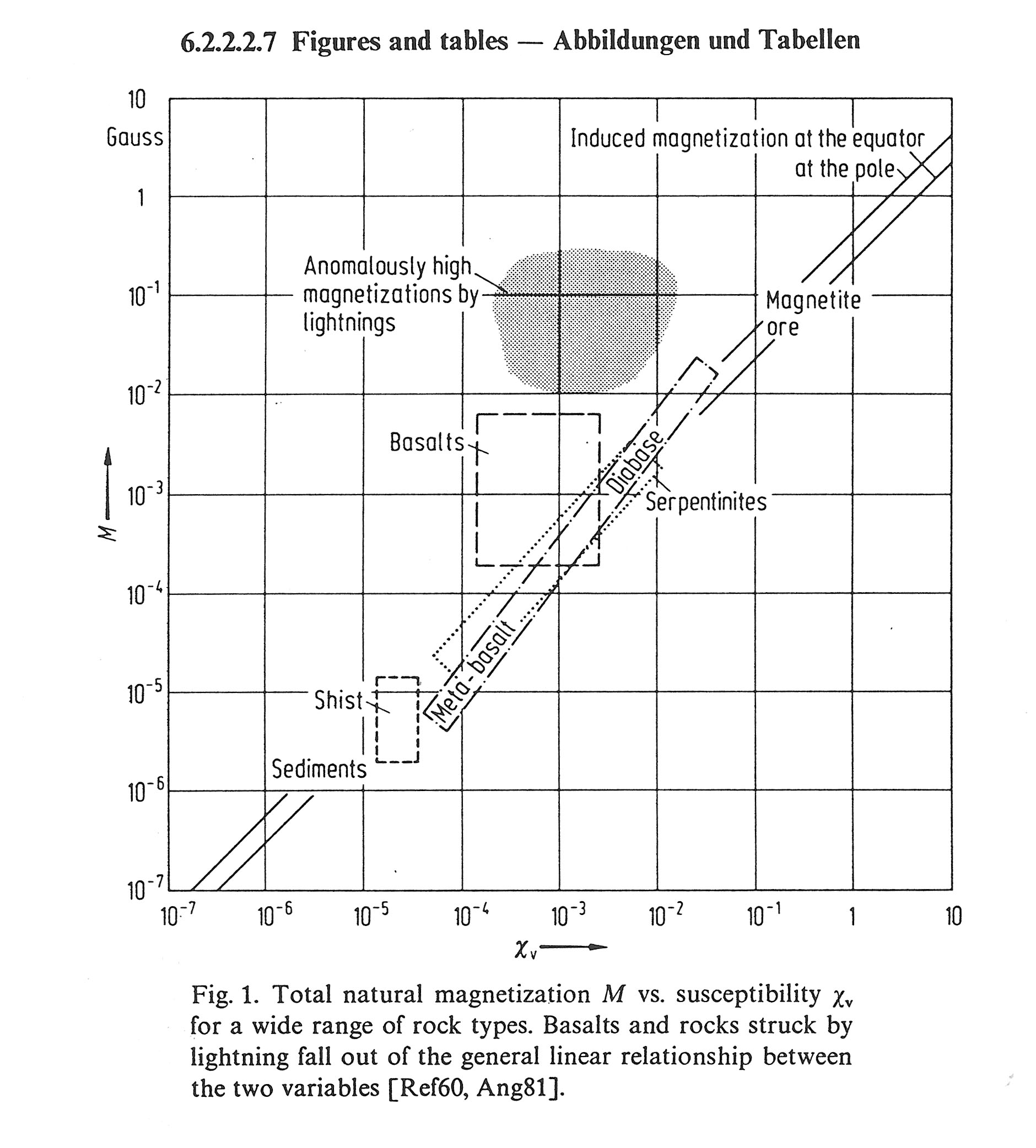
- Rock Physics and Phase Relations -A Handbook of Physical Contents, T.J.Ahrens ed., AGU, 1995より
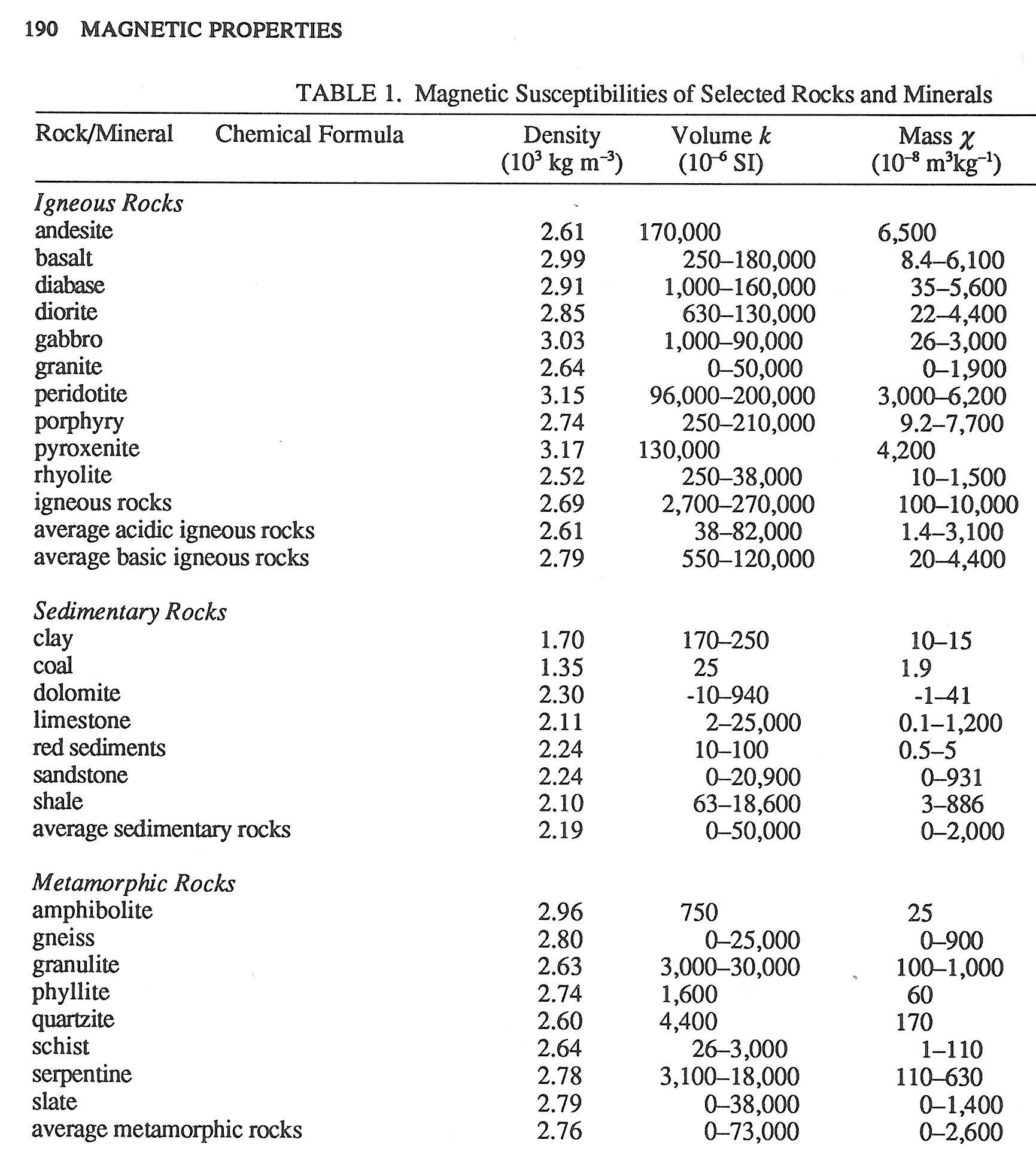
- Physical Properties of Rocks, G.Angenheister ed., Springer-Verlag, 1982より
- 磁化率を5.0×10-2SIとすると,誘導磁化は磁化率の平均値とIGRFの全磁力値(46000 nT)の掛け算になる。
0.05×46000nT=5×46×10-8(T)=23×10-7(T)
T(テスラ)はB(磁束密度)の単位で、A/mはH(磁場)とJ(磁化)の単位。よってH=B/μ0。
μ0=4π×10-7H/m、T=Wbm-2、H=WbA-1より1T={1/(4π×10-7)}A/m。ゆえに、23/(4π)=1.83A/mと計算される。
上の参考資料を見ると、5.0×10-2SI程度の磁化率の岩石は、だいたい10-3G=1A/m程度の自然残留磁化を持つことが多い。
よってこのような例では、磁場の計算には、両方を足して、2-3A/mくらいを与えることが多い。
| Quantity | SI | cgs | SI×f→cgs | cgs×f→SI |
|---|---|---|---|---|
| Magnetic induction(B) | T | G | 1[T]=1[Wbm2]×104→G | 1[T]=1[G]×10-4→[T]=100[μT] |
| Magnetic field(H) | A/m | Oe | 1[A/m]×(4π/103)→[Oe] | 1[Oe]×(103/4π)→[A/m] |
| Magnetic moment | Am2 | emu | 1[Am2]×103→[emu] | 1[emu]×10-3→[Am2] |
| Volume magnetization | A/m | emu/cc | 1[A/m]×10-3→[emu/cc] | 1[emu/cc]×103→[A/m] |
| Mass magnetization | Am2/kg | emu/g | 1[Am2/kg]×1→[emu/g] | 1[emu/g]×1→[Am2/kg] |
| Bulk susceptibility | m3 | emu/Oe | 1[m3]×(106/4π)→[emu/Oe] | 1[emu/Oe]×(4π/106)→[m3] |
| Volume susceptibility | SI | G/Oe | 1[SI]×(1/4π)→[G/Oe] | 1[G/Oe]×(4π)→[SI] |
| Mass susceptibility | m3/kg | emu/(Oe・g) | 1[m3/kg]×(103/4π)→[emu/Oe・g] | 1[emu/Oe・g]×(4π/103)→[m3/kg] |
メモ
cgsからSI単位系への移動をスムースに行うために、SI慣用系という単位が導入された。
磁場の単位としてT、磁化の単位としてA/m、が推奨された。
- 磁場はB:B=μ0(H+J)
もともと磁場HはcgsでOeだから磁束密度BのcgsでのGaussとは違う次元である。
それを慣用系では一緒にした。
- 1nT=1γ=10-5G
- 磁化はJ:磁気モーメントM(1emu=Gcm3)から単位体積当たりの磁化は、1A/m=10-3emu/ccに読みかえる。
- μ0=4π×10-7H/m
- Wb=kgm2A-1s-2 T=Wbm-2=kgA-1s-2 H=WbA-1=kgm2A-2s-2
- mass magnetization[emu/g]×density[g/cc]=volume magnetization[emu/cc]
- mass susceptibility[emu/g/Oe]××density[g/cc]×4π=volume susceptibility[G/Oe]×4π=volume susceptibility=volume susceptibility[SI]