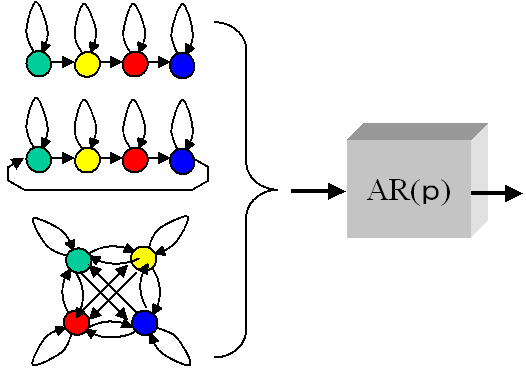
図1 ARHMMの例
以下は,厳密な議論を一切省いた、ARHMMについての簡単で直感的な説明です。
ARHMMは、図1に示すように、HMMの出力をARフィルタに通す構成となっています。

図1 ARHMMの例
HMMは、短時間の定常と見なせる区間を表現する状態を幾つかつなぎ合わせて、観測時系列の時間的な変化を表現するモデルと考えられます。
図2は、赤線で示した観測時系列を6状態のHMMで表現した例です。図中、黒線は、各状態における出力の期待値を表しています。
HMMは、状態の中で観測時系列の変化を表現できない、また定常区間と定常区間の間で統計量の不連続性が生じるなどの問題点があります。
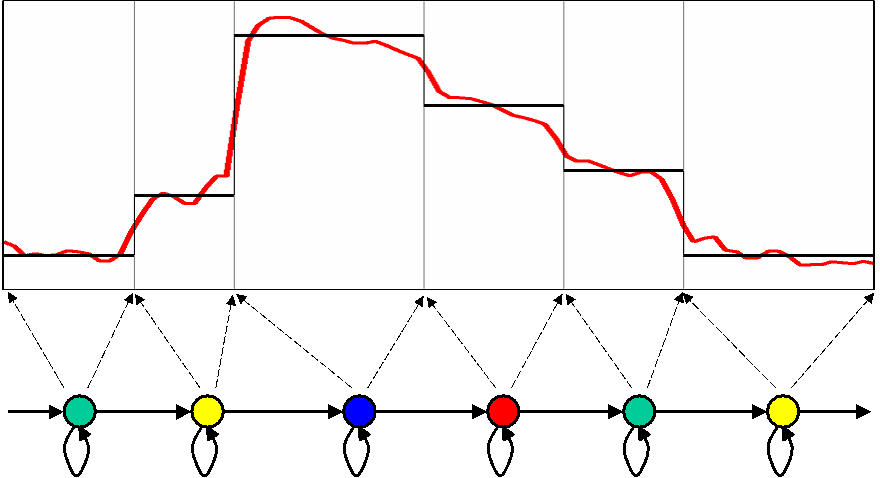
図2 HMMによる時系列のモデリング(その1)
図2の例は観測時系列が比較的に単純で緩やかに変化していますが、図3に示すようなより複雑に変化する観測時系列をHMMで表現しようとすると、より多くの状態を必要とするという問題点もあります。
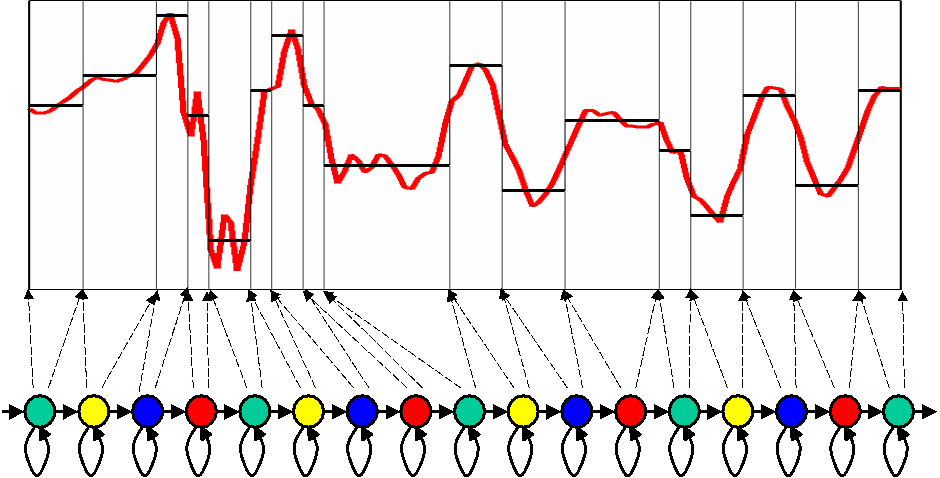
図3 HMMによる時系列のモデリング(その2)
一方、ARHMMは、観測時系列をARフィルタで逆フィルタリングした時系列をHMMで表現することになります。
観測時系列が一定の相関を持って変化している場合、その相関性をARフィルタで取り除くことで、単純な時系列に変換できる場合があります。
図4は、図3の観測時系列を実際にARHMMで分析して得られたARフィルタで、逆フィルタリングした時系列です。
このようにARHMMは、より少ない状態数で効率的に観測時系列を表現できる可能性があります。
また、ARHMMは、HMMの出力をARフィルタに通しているので、連続的に変化する統計量で観測時系列を表現していることになります。
図3の観測時系列をARHMMで表現する場合、その期待値の時系列は、図4の不連続な期待値をARフィルタでフィルタリングすることで求められるので、連続的な統計量になります。
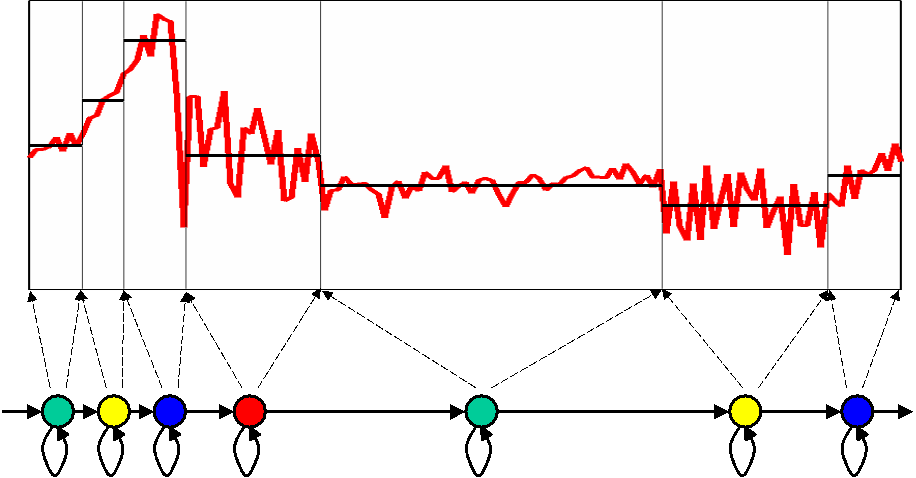
図4 ARHMMに基づいた分析により相関性を取り除いた時系列
Copyright(c) 2007 Akira Sasou All Rights Reserved.